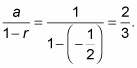Many divergent series of positive terms converge if you change the signs of their terms so they alternate between positive and negative. For example, you know that the harmonic series diverges:
But, if you change every other sign to negative, you obtain the alternating harmonic series, which converges:
By the way, this series converges to ln 2, which equals about 0.6931.
An alternating series is said to be conditionally convergent if it’s convergent as it is but would become divergent if all its terms were made positive. An alternating series is said to be absolutely convergent if it would be convergent even if all its terms were made positive. And any such absolutely convergent series is also automatically convergent as it is.
Here’s an example. Determine the convergence or divergence of the following alternating series:
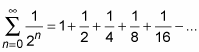
If all these terms were positive, you’d have the familiar geometric series,
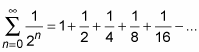
which, by the geometric series rule, converges to 2. Because the positive series converges, the alternating series must also converge and you say that the alternating series is absolutely convergent.
The fact that absolute convergence implies ordinary convergence is just common sense if you think about it. The previous geometric series of positive terms converges to 2. If you made all the terms negative, it would sum to –2, right? So, if some of the terms are positive and some negative, the series must converge to something between –2 and 2.
Did you notice that the above alternating series is a geometric series as it is with
(Recall that the formula for the sum of a geometric series works whenever r is between -1 and 1; it thus works for alternating series as well as for positive series.) The formula gives its sum: