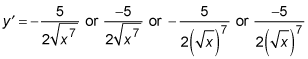According to the power rule, if you want to find the derivative of a variable raised to a power, you must bring the power in front — multiplying it by the coefficient, if there is one — and then reduce the power by one.
To see the power rule in action, take a look at the following practice questions.
Practice questions
If f (x) = 5x4, then find the derivative,
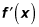
Find the derivative,
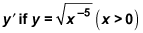
Answers and explanations
The derivative of f (x) = 5x4 is
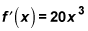
To find the derivative, bring the 4 in front and multiply it by the 5, and at the same time reduce the power by 1, from 4 to 3:
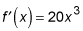
Notice that the coefficient 5 has no effect on how you do the derivative in the following sense: You could ignore the 5 temporarily, do the derivative of x4 (which is 4x3), and then put the 5 back where it was and multiply it by 4.
The derivative is
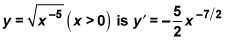
To find the derivative, first rewrite with an exponent
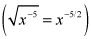
Bring the power in front and reduce the power by one:
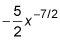
To write your answer without a negative power, you write
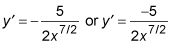
Or you can write your answer without a fraction power, to wit: