If you're given an equation for a line, you can find the points of tangency and normalcy on that line. To do this, you need to know how tangents and normal lines work:
At its point of tangency, a tangent line has the same slope as the curve it's tangent to. In calculus, whenever a problem involves slope, you should immediately think derivative. The derivative is the key to all tangent line problems.
At its point of intersection to a curve, a normal line is perpendicular to the tangent line drawn at that same point. When any problem involves perpendicular lines, you use the rule that perpendicular lines have slopes that are opposite reciprocals. So all you do is use the derivative to get the slope of the tangent line, and then the opposite reciprocal of that gives you the slope of the normal line.
Here's an example:
Find all lines through (1, –4) either tangent to or normal to y = x3. For each tangent line, give the point of tangency and the equation of the line; for the normal lines, give only the points of normalcy.
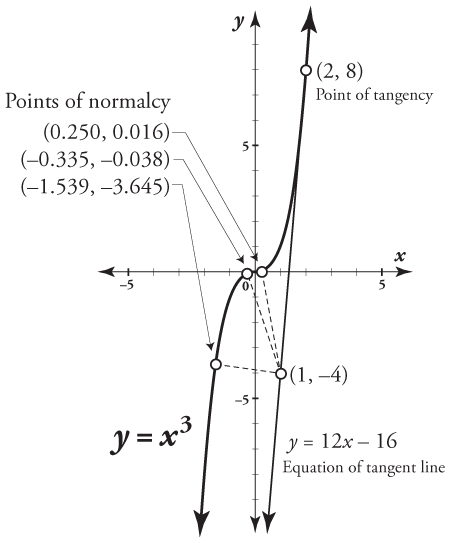
To help you out, here's a graph showing the final results:
So how do you find all this incredibly useful information? By following these handy-dandy steps:
Find the derivative.

For the tangent lines, set the slope from the general point (x, x3) to (1, –4) equal to the derivative and solve.

Plug this solution into the original function to find the point of tangency.
The point is (2, 8).
Get your algebra fix by finding the equation of the tangent line that passes through (1, –4) and (2, 8).
You can use either the point-slope form or the two-point form to arrive at y = 12x – 16.
For the normal lines, set the slope from the general point (x, x3) to (1, –4) equal to the opposite reciprocal of the derivative and solve.

Plug these solutions into the original function to find the points of normalcy.
Plugging the points into y = x3 gives you the three points: (–1.539, –3.645), (–0.335, –0.038), and (0.250, 0.016).
So, you find that the point of tangency is (2, 8); the equation of tangent line is y = 12x – 16; and the points of normalcy are approximately (–1.539, –3.645), (–0.335, –0.038), and (0.250, 0.016).





