In trying to understand what makes a function integrable, you first need to understand two related issues: difficulties in computing integrals and representing integrals as functions.
Computing integrals
For many input functions, integrals are more difficult to compute than derivatives. For example, suppose that you want to differentiate and integrate the following function:
y = 3x5e2x
You can differentiate this function easily by using the Product Rule:
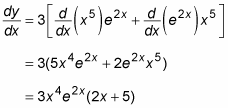
Because no such rule exists for integration, in this example you’re forced to seek another method.
Finding solutions to integrals can be tricky business. In comparison, finding derivatives is relatively simple.
Representing integrals as functions
Beyond difficulties in computation, the integrals of certain functions simply can’t be represented by using the functions that you’re used to.
More precisely, some integrals can’t be represented as elementary functions — that is, as combinations of the functions you know from Pre-Calculus.
For example, take the following function:
You can find the derivative of the function easily using the Chain Rule:
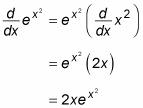
However, the integral of the same function,
can’t be expressed as a function — at least, not any function that you’re used to.
Instead, you can express this integral either exactly — as an infinite series — or approximately — as a function that approximates the integral to a given level of precision. Alternatively, you can just leave it as an integral, which also expresses it just fine for some purposes.





