Math meets fortunetelling in sequences (numbers arranged in a fixed order). The PSAT/NMSQT lords provide a set of numbers (each number is called a term) and ask you to identify another term in the sequence. They may want the next term or a term many steps along.
Sequences show up in two varieties on the PSAT/NMSQT: arithmetic (when the terms occur because of adding or subtracting) and geometric (when you multiply or divide to move from one term to another). Here are two examples of each type of sequence:
Arithmetic: 2, 10, 18, 26 . . . (add 8 to arrive at the next term)
Arithmetic: 16, 9, 2, –5 . . . (subtract 7 to arrive at the next term)
Geometric: 2, 30, 450 . . . (multiply by 15 to arrive at the next term)
Geometric: 350, 70, 14, 2.8 . . . (divide by 5 to arrive at the next term)
If you’re asked for the fourth term beyond the numbers presented, you can just calculate your way to the correct answer. If they want the 41st term in the sequence, your time will run out if you take the time to calculate all those intermediate steps. Formulas to the rescue! You can use these shortcuts to find any term in a sequence:
Call the term you’re seeking the nth term. The number of steps to get from the first term to the term you want is n – 1. So to go from the first term to, say, the 25th term, you need 24 steps.
In an arithmetic sequence, calculate the difference between terms in the sequence. In the first example, the difference (also known as d) is 8.
Apply this formula to find the nth term in an arithmetic sequence:
nth term = the first term + (n – 1)d
So in the first arithmetic sequence, the 20th term would be 2 + (20 – 1)8. When you figure it out, you get 154.
In a geometric sequence, figure out the ratio of one term to the next. Before you faint, the ratio in a geometric sequence, abbreviated as r, is just the number you’re multiplying or dividing by. In the first geometric sequence, r = 15.
Apply the formula for a geometric sequence:
nth term = the first term x r (n–1)
Okay, take another look at the first geometric sequence example, and use the formula to find the fifth term: 5th term = 2 x 15(5 – 1), which gives you 2 x 154, which gives you 2 x 50,625, which gives you 101,250. (That’s a big number, but geometric sequences grow large fast.)
On the PSAT/NMSQT you may find a sequence problem that’s all numbers, but sometimes sequences are tucked into word problems, like this one:
After your mother discovers that you cut a class on Monday, she takes away your phone for 3 days. She tells you that for every additional cut, you’ll lose the phone for 3 extra days. If you cut class every day for the rest of the week, for how many days will your connection to the outside world be suspended? And will your friends ever speak with you again?
You can just add up the numbers (3 days as of Monday, 6 days as of Tuesday, 9 as of Wednesday, 12 as of Thursday, with a grand total of 15 when you add 3 for Friday). Or, you can apply the earlier arithmetic formula. No matter which method you use, your social life is toast.
Try these practice problems:
In the following sequence, determine the value of the 17th term.
15, 11, 7, 3, . . .
(A) 0
(B) –41
(C) –45
(D) –49
(E) –53
Jose checks the population of his ant farm once per week. When he checks during the first week, he has 160 ants. During week 2, he has 240 ants; week 3 has a count of 360 ants; and week 4 has a count of 540 ants. If the ant population continues to grow like this, how many ants do you expect Jose to count during week 6?
(A) 810
(B) 1,000
(C) 1,200
(D) 1,215
(E) 1,230
In a certain geometric sequence, each term is half as large as the preceding term. If the first term has a value of 64, which term has a value of 1/4?
(A) 8th term
(B) 9th term
(C) 10th term
(D) 14th term
(E) 16th term
Now check your answers:
D. –49
You’re looking for a specific term in an arithmetic sequence, so you want to use the formula nth term = the first term + (n – 1)d. You want the 17th term, so n will be 17. The first term is 15, and the constant difference is –4 (each term is 4 less than the previous term).
Plugging these numbers into the formula: 17th term = 15 + (17 – 1)(–4) = 15 + (16)(–4) = 15 – 64 = –49, Choice (D).
D. 1,215
A geometric sequence! Did you see that each week Jose has 3/2 as many ants as he had the week before? You could use the formula for this one, but it’s probably easier to just calculate directly to the 6th week. Week 5 = 540 x 3/2 = 810 ants. Week 6 = 810 x 3/2 = 1,215 ants, Choice (D).
B. 9th term
You could always solve this problem by simply writing out the terms and counting to see which one equals 1/4 (64, 32, 16, 8, 4, 2, . . .), but in this case flex your new geometric sequence muscles and try to solve this problem algebraically.
Your key equation: nth term = the first term x r(n–1). You don’t know what n is yet, but you know that the first term is 64, r is 1/2 (because you always multiply by 1/2 to get the next term), and the nth term is 1/4.
Plug all this into the equation and you get:
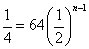
Divide both sides by 64:
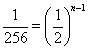
How many times do you need to multiply 2 by itself to get 256? Eight times, meaning that n – 1 is 8, so n is 9, Choice (B).

