You will encounter polygons on the PSAT/NMSQT. A polygon is a closed, two-dimensional figure with sides made of lines. In other words, a triangle, a square, a rectangle, and any other closed shape you can create by drawing lines is a polygon.
Polygons are named according to the number of sides they have: A triangle has three sides (the prefix tri means “three”), a quadrilateral has four, a pentagon has five, and so on. How high do those numbers go? Well, a megagon has a million sides, and an apeirogon has an infinite number of sides.
These facts may help you in a trivia contest, but you don’t need them for the PSAT/NMSQT. In fact, you don’t need vocabulary to handle polygons, just math.
These concepts help you deal with polygons when you encounter them on the exam:
The sum of the angles inside a four-sided figure equals 360º. Add up the angles inside a square, rectangle, parallelogram, or any other quadrilateral and you get 360º.
Squares and rectangles have right angles. A square has four sides of the same length; a rectangle has two long sides that are equal and two short sides that are equal. Each corner is a right angle (90º). To find the area, multiply length by width. (Note: The area formula is in the information box on the exam.)
In a parallelogram, the top and bottom sides are parallel and equal, as are the left and right sides. Technically, squares and rectangles are parallelograms, but you can also have a parallelogram without right angles. Imagine a square or a rectangle slipping sideways. That’s a parallelogram.
To find the area of a parallelogram, multiply the base by the height. To find the height, measure a perpendicular line from the tallest point to the base, as in this figure:

Notice that the top and bottom lines in this figure have little double slash marks on them. Those marks tell you that the lines are parallel. When you take the PSAT/NMSQT, don’t assume that lines are parallel unless the question tells you so with words or with this symbol.
On the PSAT/NMSQT you may have to find the area of a polygon. (Check the information box if you need help remembering the formulas.) You may also be asked to find the perimeter, the sum of the lengths of all the sides.
Often, the easiest way to deal with polygons (especially strangely shaped polygons) is to divide them into triangles, as in this diagram:
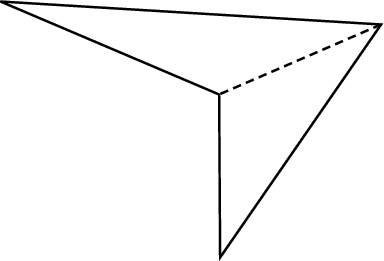
Notice the broken line? It divides this shape into two triangles. Because you know how to figure out the area, perimeter, sides, and angles of a triangle, you can handle whatever you’re asked about this figure.
When you divide a polygon into triangles, remember that the sum of the angles in each triangle equals 180°. If you’re asked to find the sum of the interior (inside) angles of a polygon, multiply the number of triangles by 180°. In this figure, for example, you have two triangles, for a total of 360°.
In the following figure, determine the value of


(A) 108°
(B) 120°
(C) 180°
(D) 210°
(E) 540°
In parallelogram ABCD, AB is parallel to CD, and AB = CD = 6. If the area of parallelogram ABCD is 30, how far apart are AB and CD?
(A) 2.5
(B) 5
(C) 10
(D) 15
(E) 20
What is the area of the quadrilateral ABCD? Note that sides AD and BC are parallel.

(A) 9
(B) 10
(C) 11
(D) 12
(E) 13
Now check your answers.
C. 180°
You know that there are 180° in a triangle, so pick a corner of the polygon and draw lines to divide it into triangles.

Now it’s easy to see that you have three triangles, meaning that the angles add up to 3 x 180° = 540°. You want to know what the sum of the angles divided by 3 is, so you’re back at 180°, Choice (C).
B. 5
Draw a picture! After you have your picture, it’s easy to see that the distance between AB and CD is really the height of the parallelogram. To find the area of a parallelogram, you multiply the base by the height, and you already know the area and the base! A = bh, 30 = 6h, h = 5, Choice (B).

D. 12
If you happen to know the formula for the area of a trapezoid, you’re all set.

If not, you can think of the polygon as a rectangle inserted into a triangle, as deconstructed here:

The area of the square is 3 x 3 = 9, and the triangle has a base of 5 – 3 = 2 and a height of 3, making an area of 1/2(2)(3) = 3. Add those areas together and you get 9 + 3 = 12, Choice (D).




