Each data sufficiency problem poses a question, followed by two statements. Your task is to evaluate the statements to determine at what point there is or is not sufficient information to answer the question.
Unlike the problem solving questions, you do not actually have to answer the question posed. Instead, you select one of five fixed answer choices that offer different options about the sufficiency of the information provided in the two statements.
Practice questions
- A retail store sent out a promotional offer to 300 former customers and 700 potential customers. What percent of the total number of people who received the promotional offer gave a favorable response?(1) The store received a favorable response from 30 percent of the former customers.(2) The store received a favorable response from 20 percent of the potential customers.
A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C. Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient to answer the question asked.
D. Each statement ALONE is sufficient to answer the question asked.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked.
- If a sequence A has 200 terms, what is the 100th term of A?(1) The first term of sequence A is .
(2) Each term of sequence A after the first term is 15 more than the preceding term.A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C. Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient to answer the question asked.
D. Each statement ALONE is sufficient to answer the question asked.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked.
Answers and explanations
- The correct answer is C.Let F = the number of favorable responses from former customers and P = the number of favorable responses from potential customers. Then the percent of favorable responses is
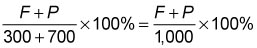
From (1), , which you can substitute into

The value of this quantity can vary, so without additional information, you cannot determine an exact value of
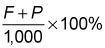
Thus, (1) is not sufficient. From (2), P = 20% (700) = 140, which you can substitute into

The value of this quantity can vary, so without additional information, you cannot determine an exact value of
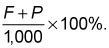
Thus, (2) is not sufficient.
Taking (1) and (2) together,
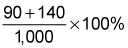
Therefore, both statements together are sufficient, but neither statement alone is sufficient.
- The correct answer is C.Let a1 = the first term of sequence A, and a100 = the hundredth term of sequence A. From (1), a1 = –10. But without additional information, you cannot determine subsequent terms, including an exact value of a100. Thus, (1) is not sufficient.From (2), a1 = a1, a2 = a1 + 15, a3 = a1 + (2)(15), a4 = a1 + (3)(15), and so on. Hence, a100 = a1 + (99)(15). But without additional information, you cannot determine an exact value of a100. Thus, (2) is not sufficient.
Taking (1) and (2) together, the exact value of the 100th term is a100 = (–10) + (99)(15). Therefore, both statements together are sufficient, but neither statement alone is sufficient.

