The Geometry of the Chessboard

You were probably taught that a straight line is the shortest distance between two points. While this is a geometric fact (not counting wormholes) in everyday life, it's a geometric option on the chess board. Distance is counted on the chessboard not by inches, feet, or parsecs, but by squares.

You may need to get from Point A on the chessboard to Point B, but your opponent may not want you there. They may block one or two of your pathways during the endgame, so checking out all the possible routes is wise. You have fewer alternatives in the endgame, by definition, so it can become possible to consider all of them.

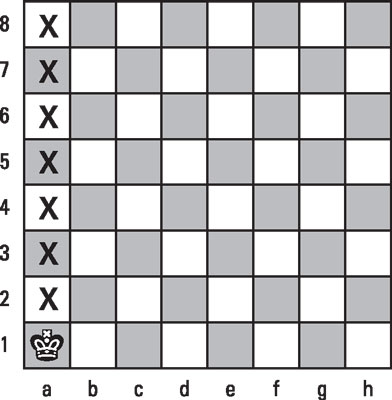
Consider the case of the king, who's instrumental during the endgame. The king moves one square at a time in any direction. If you think that the shortest route from a1 to a8 in this figure is to move the king in a straight line, you're correct. However, alternatives exist that are just as short.

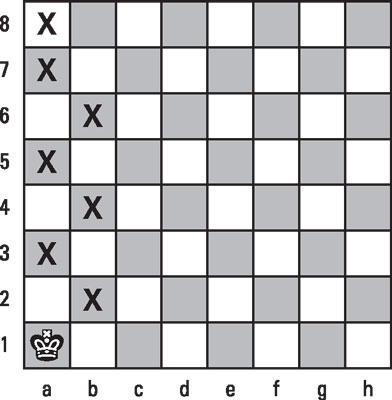
The path a1-b2-a3-b4-a5-b6-a7-a8, shown in the following figure, is just as short. Getting from a1 to a8 takes seven moves if you march in a straight line and seven moves if you skate from side to side! As long as you get where you're going in the same number of moves, it doesn't matter how you do it.

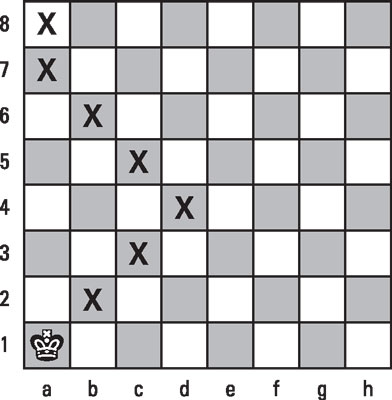
The least intuitive method may be the one shown in the following figure. The king first marches toward the center (d4), and only then makes a dash to a8.

All these methods are equivalent in that they take seven moves, but considering your alternatives before deciding on a course of action is important because only one of them may lead to victory.