In physics, when you rotate an extended object, such as a rod, disk, or cube, which has its mass distributed through space, you have to take into account where the force is applied. Enter torque. Torque is a measure of the ability of a force to cause rotation. In physics terms, the torque exerted on an object depends on the force itself (its magnitude and direction) and where you exert the force. You go from the strictly linear idea of force as something that acts in a straight line (such as when you push a refrigerator up a ramp) to its angular counterpart, torque.
Just as a net force causes acceleration, a net torque causes angular acceleration, so you can think of torque as the angular equivalent of force.
Torque brings forces into the rotational world. Most objects aren’t just points or rigid masses, so if you push them, they not only move but also turn. For example, if you apply a force tangentially to a merry-go-round, you don’t move the merry-go-round away from its current location — you cause it to start spinning.
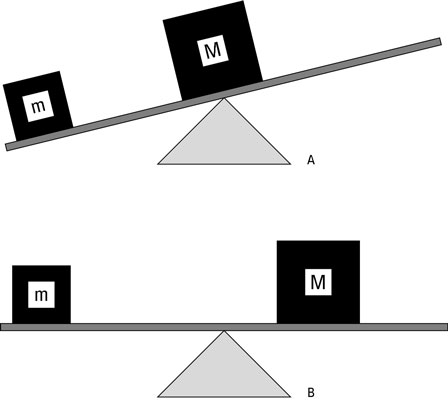
The figure shows a seesaw with a mass m on it. If you want to balance the seesaw, you can’t have a larger mass, M, placed on a similar spot on the other side of the seesaw. Where you put the larger mass M determines whether the seesaw balances. As you can see in diagram A, if you put the mass M on the pivot point — also called the fulcrum — of the seesaw, you don’t have balance. The larger mass exerts a force on the seesaw, but the force doesn’t balance it.
As you can see in diagram B, as you increase the distance you put the mass M away from the fulcrum, the balance improves. In fact, if M = 2m, you need to put the mass M exactly half as far from the fulcrum as the mass m is.
The torque is a vector. The magnitude of the torque tells you the ability of the torque to generate rotation; more specifically, the magnitude of the torque is proportional to the angular acceleration it generates. The direction of the torque is along the axis of this angular acceleration.





