Mass, velocity, and radius are all related when you calculate centripetal force. In fact, when you know this information, you can use physics equations to calculate how much force is required to keep an object moving in a circle at the same speed.
You always have to accelerate an object toward the center of the circle to keep it moving in circular motion. If an object is moving in uniform circular motion at speed v and radius r, you can find the magnitude of the centripetal acceleration with the following equation:
Because force equals mass times acceleration, F = ma, and because centripetal acceleration is equal to v2/r, you can determine the magnitude of the centripetal force needed to keep an object moving in uniform circular motion with the following equation:
This equation tells you the magnitude of the force that you need to move an object of a given mass, m, in a circle at a given radius, r, and linear speed, v. (Remember that the direction of the force is always toward the center of the circle.)
Think about how force is affected if you change one of the other variables. The equation shows that if you increase mass or speed, you’ll need a larger force; if you decrease the radius, you’re dividing by a smaller number, so you’ll also need a larger force. Here’s how these ideas play out in the real world:
Increasing mass. You may have an easy time swinging a golf ball on a string in a circle, but if you replace the golf ball with a cannonball, watch out. You may now have to whip 10 kilograms around on the end of a 1.0-meter string every half-second. As you can tell, you need a heck of a lot more force.
Increasing speed. Not interested in spinning cannonballs? Then imagine you’re driving your car around in a circle. If you’re going quite slowly around the circle, your tires have no problem generating enough frictional force to keep you going in the circle. But if you go too fast, then your tires can no longer generate the frictional force acting toward the center of the circle, so you start to skid.
Decreasing the radius. You can see the effect of the radius in your car going around in a circle. If you drive your car at a fixed speed in a circle of smaller and smaller radius, eventually your tires won’t be able to supply enough centripetal force from the friction, and you’ll skid off the circular path.
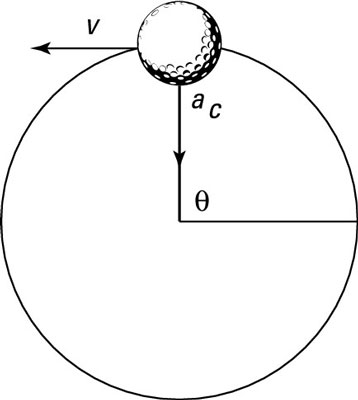 A golf ball on a string traveling with constant speed.
A golf ball on a string traveling with constant speed.
Here’s an example: The ball from the figure is moving at 12.6 meters/second on a 1.0-meter string. How much force do you need to make a 10.0-kilogram cannonball move in the same circle at the same speed? Here’s what the equation looks like:
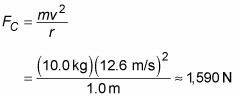
You need about 1,590 newtons, or about 357 pounds of force (4.448 newtons are in a pound). Pretty hefty!





