Using physics, you can calculate the centripetal force of objects that are moving in a circle. The following examples show you how the centripetal force on a revolving object is affected by the object's mass, speed, and distance from the center.
Practice questions
You sit on a stool, stick your legs straight out in front of you, and spin around. If you complete 3 revolutions in 9.0 seconds and your legs are 0.85 meters long, what is the centripetal force in newtons on your big toe?
Assume that the mass of your big toe is 0.035 kilograms.
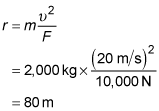
In a prototype helicopter, a jet is expelled out of the helicopter's side to make it turn in the opposite direction. If the jet supplies 10,000 newtons of force and the helicopter's forward speed remains at 20 meters per second, what is the radius in meters of the helicopter's turn?
Assume the mass of the helicopter is 2,000 kilograms.
Answers
The following are the answers to the practice questions:
0.13 N
You complete 3 revolutions in
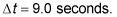
Each revolution is

so your angular speed is
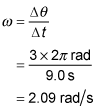
The equation for centripetal acceleration is
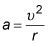
The tangential speed
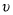
is related to angular speed by
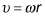
so the equation for centripetal acceleration becomes
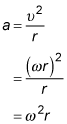
Use this equation for acceleration in Newton's second law to find the centripetal force on your big toe:
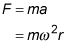
Plug in r = 0.85 meters, m = 0.035 kilograms, and the angular speed from earlier to find the answer:
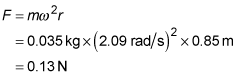
80 m
From Newton's second law, force is related to acceleration by F = ma where m is the mass of the object being accelerated. The acceleration in this case is the centripetal acceleration, which is related to tangential speed by
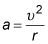
where r is the radius of the curve through which the object moves. Combining these two equations to eliminate the acceleration gives
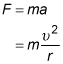
Solving this equation for the radius of the turn gives
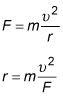
In this case, F = 10,000 newtons,

and m = 2,000 kilograms. Plugging these values into the earlier equation gives