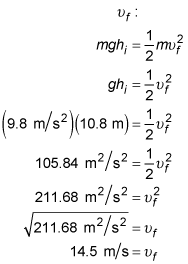In physics, you can convert kinetic energy into potential energy and back again using conservation of energy. For example, you can calculate the kinetic energy of a bowling ball just before it falls to the ground.
Here are some practice questions that you can try.
Practice questions
A bowling ball is lifted to a height such that its gravitational potential energy is 20 joules relative to the ground. If released from rest, how much kinetic energy does the ball have just before striking the ground?
Ignore air resistance.
A gust of wind shakes loose a football that was stuck in a tree. Ignoring air resistance, if the football falls from a height of 10.8 meters, what is its speed just before hitting the ground?
Round your answer to the nearest tenth of a meter per second.
Answers
The following are the answers to the practice questions:
20 J
In the absence of friction, mechanical energy is conserved:
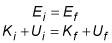
where K is kinetic energy and U is potential energy. The ball is released from rest, so its initial velocity is 0, meaning that its initial kinetic energy is also
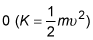
If the ground is designated with a value of 0 meters for h, then the final potential energy (gravitational) is also 0. Thus, the equation simplifies to
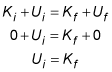
The final kinetic energy is equal to the initial potential energy of 20 joules.
14.5 m/s
In the absence of friction, mechanical energy is conserved:
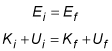
where K is kinetic energy and U is potential energy. The football is initially at rest, and it has no kinetic energy at that point; its velocity is 0. If the height of the ground is designated as 0 meters, then the final gravitational potential energy is also 0. Thus, the equation simplifies to
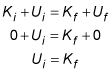
When the equations for kinetic and gravitational potential energy are substituted, this becomes
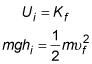
where m is the mass, hi is the initial height, g is the acceleration due to gravity near Earth's surface, and
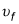
is the final velocity (in this case, when the height equals zero). Substitute the correct values after cancelling the m from both sides to solve for