The trig function cosine, abbreviated cos, works by forming this ratio: adjacent/hypotenuse. In the figure, you see that the cosines of the two angles are as follows:


The situation with the ratios is the same as with the sine function — the values are going to be less than or equal to 1 (the latter only when your triangle is a single segment or when dealing with circles), never greater than 1, because the hypotenuse is the denominator.
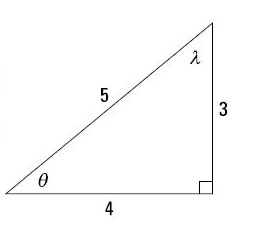
The two ratios for the cosine are the same as those for the sine — except the angles are reversed. This property is true of the sines and cosines of complementary angles in a right triangle (meaning those angles that add up to 90 degrees).
If theta and lambda are the two acute angles of a right triangle, then sin theta = cos lambda and cos theta = sin lambda.
Now for an example. To find the cosine of angle beta in a right triangle if the two legs are each
feet in length:
Find the length of the hypotenuse.
Using the Pythagorean theorem, a2 + b2 = c2, and replacing both a and b with the given measure, solve for c.

The hypotenuse is

feet long.
Use the ratio for cosine, adjacent over hypotenuse, to find the answer.





