The trigonometry equations that require finding a greatest common factor, factoring it out, and then solving the equation could look like one of the following two equations:
Both of these equations are solved here.
Factor out sin x from each of the two terms.

Set the two different factors equal to 0.

Solve for the values of x that satisfy both equations. Use a scientific calculator.

All these values are solutions for the original equation. The complete list is x = 0°, 60°, 180°, 300°.

Move the term on the right to the left by subtracting it from each side.
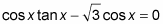
A common error in algebra — which could carry over in trig — is to divide each side by the common factor. You should never do that, because you’ll lose part of the solution.
Factor out the cos x from each term.

You don’t want to divide each side by cos x, because you’ll lose a solution if you do.
Set the two different factors equal to 0.

Solve for the values of x that satisfy both equations.

So the solutions are all of the form x = 90° + 180°n or x = 60° + 180°n.





