You can approximate, fairly accurately, the sine and cosine of angles with an infinite series, which is the sum of the terms of some sequence, or list, of numbers. Take note, however, that the series for sine and cosine are accurate only for angles from about –90 degrees to 90 degrees.
The series for the sine of an angle is
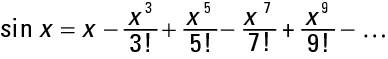
and the series for the cosine of an angle is
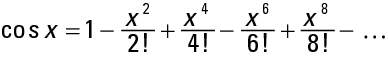
To use these formulas, you have to write the angle measure, x, in radians and carry out the computations several places. The exclamation points in the formulas don’t mean “Oh, goodness! It’s a 3!”
The exclamation points are mathematical operations called factorials. Factorial means to multiply that number times every positive integer smaller than it.
Going back to the series for the sine, an angle of 30 degrees is about 0.5236 radians. To find sin 0.5236, use the formula to get
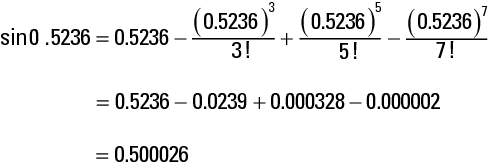
The result is pretty close to the sine of 30 degrees, which is
Carrying out the computations using a few more terms will make the result even closer to the actual answer. And the closer the angle measure is to 0, the more quickly the value of the sine or the cosine meets the exact value (the fewer terms are necessary for the answer).




