Each of the angles in a unit circle has a reference angle, which is always a positive acute angle (except the angles that are already positive and acute). By identifying the reference angle, you can determine the function values for that reference angle and, ultimately, the original angle.
Usually, solving for the reference angle first is much easier than trying to determine a trig function for the original angle. The trig functions have values that repeat over and over; sometimes those values are positive, and sometimes they’re negative.
Using a reference angle helps keep the number of different values to a minimum. You just assign the positive or negative sign after determining a numerical value for the function from the reference angle.
You determine a reference angle by looking at the terminal side of the angle you’re working with and its relation with the positive or negative x-axis (depending on which quadrant the terminal side is in). The following will tell you how to measure the reference angle when you’re given the terminal side of the angle:
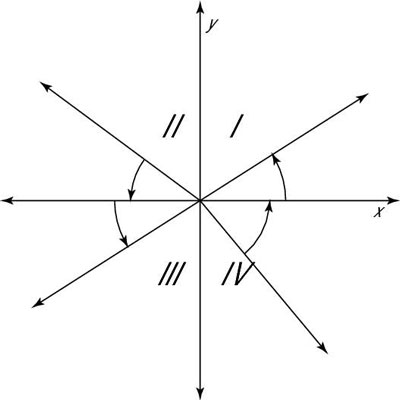
Quadrant I (QI): The reference angle is the same as the original angle itself.
Quadrant II (QII): The reference angle is the measure from the terminal side down to the negative x-axis.
Quadrant III (QIII): The reference angle is the measure from the negative x-axis down to the terminal side.
Quadrant IV (QIV): The reference angle is the measure from the terminal side up to the positive x-axis.
The figure shows the positions of the reference angles in the four quadrants.
As with all angles, you measure reference angles in degrees or radians. You might sometimes prefer to work in degrees and convert a radian measure to do these computations. Whichever method you choose is fine — it’s all a matter of taste.

