Calculating trig functions of angles within a unit circle is easy as pie. The figure shows a unit circle, which has the equation x2 + y2 = 1, along with some points on the circle and their coordinates.
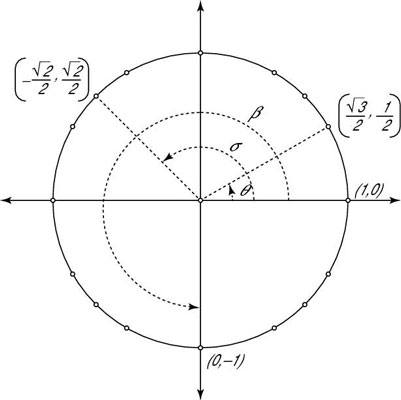
Using the angles shown, find the tangent of theta.
Find the x- and y-coordinates of the point where the angle’s terminal side intersects with the circle.
The coordinates are


The radius is r = 1.
Determine the ratio for the function and substitute in the values.
The ratio for the tangent is y/x, so you find that

Next, using the angles shown, find the cosine of sigma.
Find the x- and y-coordinates of the point where the terminal side of the angle intersects with the circle.
The coordinates are


the radius is r = 1.
Determine the ratio for the function and substitute in the values.
The ratio for the cosine is x/r, which means that you need only the x-coordinate, so

Now, using the angles shown, find the cosecant of beta.
Find the x- and y-coordinates of the point where the terminal side of the angle intersects with the circle.
The coordinates are x = 0 and y = –1; the radius is r = 1.
Determine the ratio for the function and substitute in the values.
The ratio for cosecant is r/y, which means that you need only the y-coordinate, so





