The domain of a function consists of all the input values that a function can handle — the way the function is defined. Of course, you want to get output values (which make up the range) when you enter input values.
But sometimes, when you input something that doesn’t belong in the function, you end up with some impossible situations. In these cases, you need to limit what you put into the function — the domain has to be restricted.
For example, the cosecant is defined as the hypotenuse divided by the opposite side. If the terminal side of the angle is on the x-axis, then the opposite side is 0, and you’re asked to divide by 0. Impossible!
Trig functions have domains that are angle measures (the inputs are all angles), either in degrees or radians. The outputs of the trig functions are real numbers.
The hitch here is that the different trig functions have different domains and ranges. You can’t put just any angle into some of the functions. Sine and cosine are very cooperative and have the same domain and range. The tangent function and the reciprocal functions, however, all differ.
The best way to describe these different domains and ranges is visually: Refer to the coordinate plane with a circle centered at the origin and a right triangle inside it, formed by dropping a line from any point (x,y) on the circle to the x-axis.
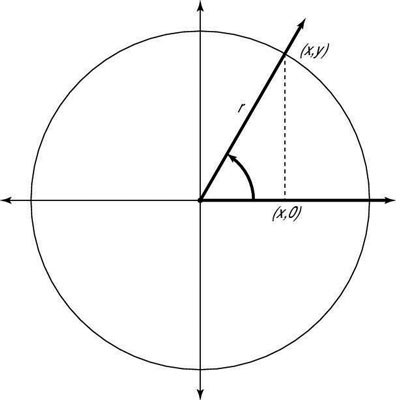
Remember that r stands for the radius of the circle (and also the hypotenuse of the right triangle in this figure).When that hypotenuse lies along one of the axes, one of the sides of the triangle is equal to 0, which is a no-no in the denominator of a fraction.
Consider the values of the variables in relation to one another. The radius, r, is always positive. And the absolute values of x and y (the lengths of the segments they represent) are always smaller than r, unless the point (x,y) is on one of the axes — then one of the values is equal to r and the other is equal to 0.




