Every triangle has six parts: three sides and three angles. If you measure the sides and then pair up those measurements (taking two at a time), you have three different pairings. Do division problems with the pairings — changing the order in each pair — and you have six different answers. These six different answers represent the six trig functions.
For example, if your triangle has sides measuring 3, 4, and 5, then the six divisions are 3/4, 4/3, 3/5, 5/3, 4/5, and 5/4.
The six trig functions are named sine, cosine, tangent, cotangent, secant, and cosecant. Many people confuse the spoken word sine with sign — you can't really tell the difference when you hear it unless you're careful with the context. You can “go off on a tangent” in some personal dealings, but that phrase has a whole different meaning in trig.
Cosigning a loan isn't what trig has in mind, either. The other three ratios are special to trig speak — you can't confuse them with anything else.
Interpreting trig abbreviations
Even though the word sine isn’t all that long, you have a three-letter abbreviation for this trig function and all the others. Mathematicians find using abbreviations easier, and those versions fit better on calculator keys. The functions and their abbreviations are
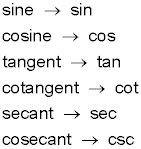
As you can see, the first three letters in the full name make up the abbreviations, except for cosecant.
Noting notation
Angles are the main focus in trigonometry, and you can work with them even if you don't know their measure. Many angles and their angle measures have general rules that apply to them. You can name angles by one letter, three letters, or a number, but to do trig problems and computations, mathematicians commonly refer to the angle names and their measures with Greek letters.
The most commonly used letters for angle measures are α (alpha), β (beta), γ (gamma), and θ (theta). Also, many equations use the variable x to represent an angle measure.
Algebra has conventional notation involving superscripts, such as the 2 in x2. In trigonometry, superscripts have the same rules and characteristics as in other mathematics. But trig superscripts often look very different. The following figure shows how you use superscripts in trig.

The first entry shows how you can save having to write parentheses every time you want to raise a trig function to a power. This notation is neat and efficient, but it can be confusing if you don't know the “code.”
The second entry shows you how to write the reciprocal of a trig function. It means you should take the value of the function and divide it into the number 1. The last entry shows how you write the inverse sine function. Using the –1 superscript between sine and the angle means that you're talking about inverse sine (or arcsin), not the reciprocal of the function.
Functioning with angles
The functions in algebra use many operations and symbols that are different from the common add, subtract, multiply, and divide signs in arithmetic. For example, take a look at the square-root operation:
Putting 25 under the radical (square-root symbol) produces an answer of 5. Other operations in algebra, such as absolute value, factorial, and step-function, are used in trigonometry, too. But the world of trig expands the horizon, introducing even more exciting processes.
When working with trig functions, you have a whole new set of values to learn or find. For instance, putting 25 into the sine function looks like this: sin 25. The answer that pops out is either 0.423 or –0.132, depending on whether you're using degrees or radians.
You can't usually determine or memorize all the values that you get by putting angle measures into trig functions. So, you need trig tables of values or scientific calculators to study trigonometry.
In general, when you apply a trig function to an angle measure, you get some real number (if that angle is in its domain). Some angles and trig functions have nice values, but most don't. The following figure shows the trig functions for a 30-degree angle.

Some characteristics that the entries confirm are that the sine and cosine functions always have values that are between and including –1 and 1. Also, the secant and cosecant functions always have values that are equal to or greater than 1 or equal to or less than –1.




