In a nutshell, the Central Limit Theorem says you can use the normal distribution to describe the behavior of a sample mean even if the individual values that make up the sample mean are not normal themselves. But this is only possible if the sample size is “large enough.” Many statistics textbooks would tell you that n would have to be at least 30.
But why is n = 30 the benchmark? Many variables in nature, finance, and other applications have a distribution that’s very close to the normal curve. For example, by looking at the t-table, you see that the various values of t start to get really close to the values of z by the time you hit about 30 degrees of freedom. One reason for this is that the t-distributions and the normal distribution share two important characteristics: They are symmetric, and they are unimodal (having one peak).
If the distribution of your individual data values is far off from either of these qualities, you might need more than a sample size of 30 to use the Central Limit Theorem. The further away the data is from being symmetric and unimodal, the more data you’ll need.
Symmetry
If you know or suspect that your parent distribution is not symmetric about the mean, then you may need a sample size that’s significantly larger than 30 to get the possible sample means to look normal (and thus use the Central Limit Theorem).
Consider the following right-skewed histogram, which records the number of pets per household.
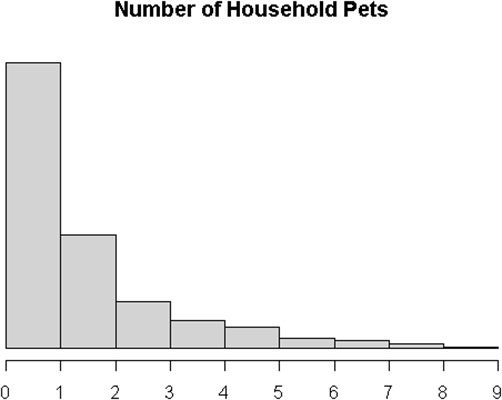
Now, suppose it represents the entire population of households. You repeatedly sample n = 30 households from that population. Here is what distribution of possible sample means looks like.
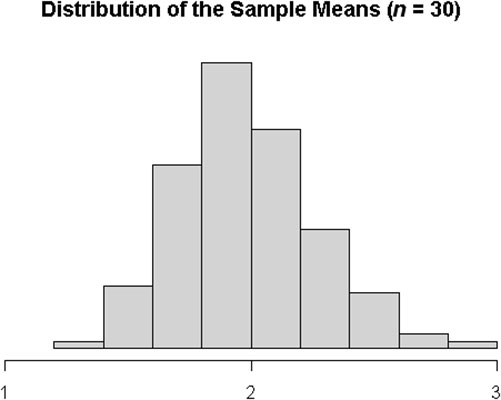
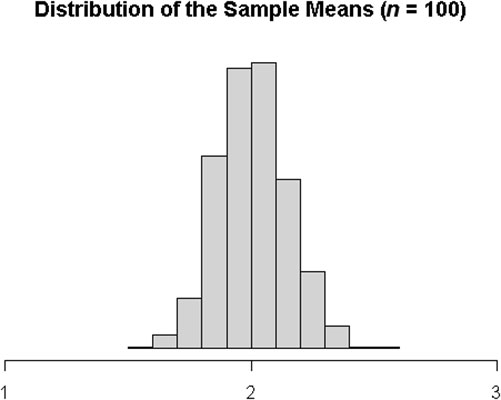
You can see that this distribution is not normal because the right tail still stretches out farther from the central peak than the left tail does. It’s not symmetric. For this population, you need to take a sample of around n = 100 to get the sample means to settle into a symmetric curve.
Unimodal
If you know or suspect that your parent distribution is not unimodal and has more than one peak, then you might need more than 30 in your sample to feel good about using the Central Limit Theorem.
Consider the following multimodal population histogram with three distinct peaks.
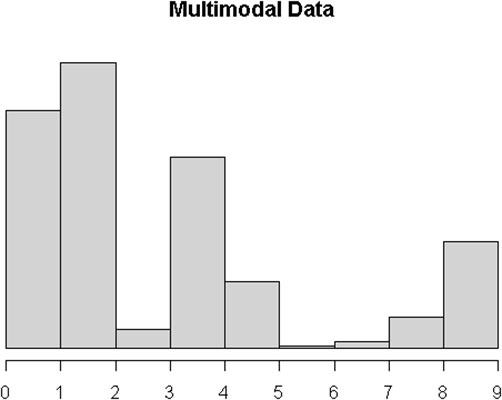
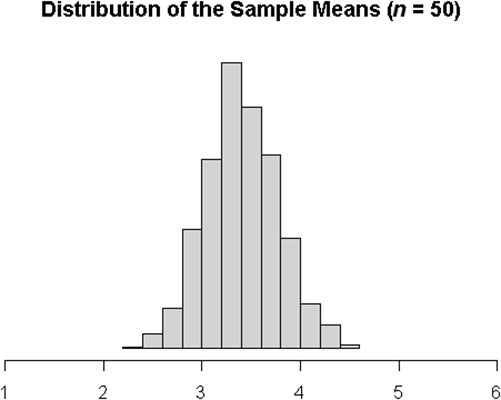
If you only sample n = 30 from that population, you do get a unimodal distribution, but it’s still not quite symmetric.
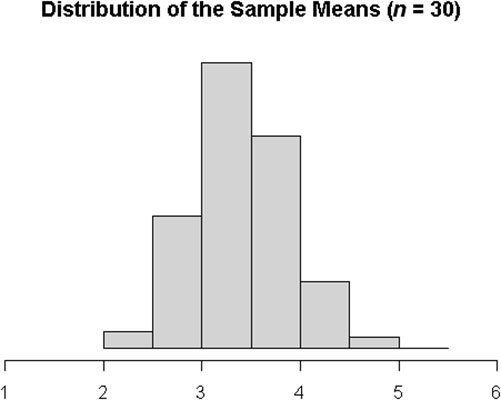
For this population, you need to take a sample of at least n = 50 to feel comfortable that your sample mean distribution is roughly normal.