How to Guess and Check Real Roots — 3 — Testing Roots by Dividing Polynomials Using Synthetic Division

Once you have used the rational root theorem to list all the possible rational roots of any polynomial, the next step is to test the roots. One way is to use synthetic division. Synthetic division is a shortcut for long division of polynomials. It’s a special case of division when the divisor is a linear factor of the form x + c, where c is a constant.

Unfortunately, the shortcut only works if the divisor (x + c) is a first-degree binomial with a leading coefficient of 1 (you can always make it 1 by dividing everything by the leading coefficient first). Luckily, you can always use synthetic division to figure out if a possible root is actually a root.

Here are the general steps for synthetic division:

1. Make sure the polynomial is written in descending order.

   The term with the highest exponent comes first.

2. Write down the coefficients and the constant of the polynomial from left to right, filling in a zero form terms of any degree that are missing; place the root you’re testing outside the synthetic division sign.

   The division sign looks like the left and bottom sides of a rectangle. Leave room below the coefficients to write another row of numbers.

3. Drop down the first coefficient below the division sign.

4. Multiply the root you’re testing by the number you just dropped down and write the answer below the next coefficient.

5. Add the coefficient and product from Step 4 and put the answer below the line.

6. Multiply the root you’re testing by the answer from Step 5 and put the product below the next coefficient.

7. Continue multiplying and adding until you use the last number inside the synthetic division sign.

   If you get a remainder, the number you tested isn’t a root.

   If the answer is 0, congratulations! You’ve found a root. The numbers below the synthetic division sign are the coefficients of the quotient polynomial. The degree of this polynomial is one less than the original (the dividend), so the exponent on the first x term should be one less than what you started with.

Say that you testing the roots for the equation, f(x) = 2x⁴ – 9x³ – 21x² + 88x + 48, and you have eliminated x = 2 by using long division, so you know not to start there. So, you decide to do synthetic division, as shown in the figure for x = 4.

The synthetic division shortcut when testing possible roots.

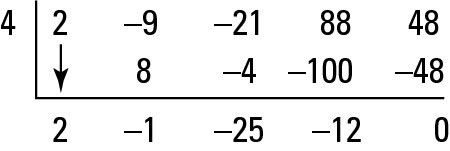
The 4 on the outside in the figure is the root you’re testing. The numbers on the inside are the coefficients of the polynomial. Here’s the synthetic process, step by step:

1. The 2 below the line just drops down from the line above.

2. Multiply 4 with 2 to get 8 and write that under the next term, –9.

3. Add –9 + 8 to get –1.

4. Multiply 4 with –1 to get –4, and write that under the –21.

5. Add –21 + –4 to get –25.

6. Multiply 4 with –25 to get –100, and write that under 88.

7. Add 88 to –100 to get –12.

8. Multiply 4 with –12 to get –48, and write that under 48.

9. Add 48 to –48 to get 0.

All you do is multiply and add, which is why synthetic division is the shortcut. The last number, 0, is your remainder. Because you get a remainder of 0, x = 4 is a root.

The other numbers are the coefficients of the quotient, in order from the greatest degree to the least; however, the quotient is always one degree lower than the degree of the original polynomial. So the quotient in this example is 2x³ – x² – 25x – 12.

Whenever a root works, you should always automatically test it again in the answer quotient to see if it’s a double root, using the same process. A double root occurs when a factor has a multiplicity of two. A double root is one example of multiplicity. You test x = 4 again, as shown in the figure.

Testing an answer root again, just in case it’s a double root.

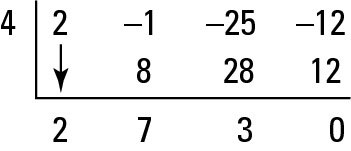
Whaddya know? You get a remainder of 0 again, so x = 4 is a double root. (In math terms, you say that x = 4 is a root with multiplicity of two.) You have to check it again, though, to see if it has a higher multiplicity. When you synthetically divide x = 4 one more time, it doesn’t work. The next figure illustrates this failure. Because the remainder isn’t 0, x = 4 isn’t a root again.

Testing the root again shows that it’s only a double root as far as the multiplicity goes.

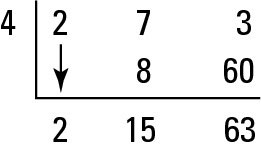
Always work off the newest quotient when using synthetic division. This way, the degree gets lower and lower until you end up with a quadratic expression, or until you have exhausted all possible rational roots. If a quadratic expression remains, you can solve the quadratic by using techniques such as factoring, completing the square, or the quadratic formula.

Before you tested x = 4 for a final time, the polynomial (called a depressed polynomial) was down to a quadratic: 2x² + 7x + 3. If you factor this expression, you get (2x + 1)(x + 3). This gives you two more roots of –1/2 and –3. To sum it all up, you’ve found x = 4 (multiplicity two), x = –1/2, and x = –3. You found four complex roots — two of them are negative real numbers, and two of them are positive real numbers.

The remainder theorem says that the remainder you get when you divide a polynomial by a binomial is the same as the result you get from plugging the number into the polynomial. For example, when you used long division to divide by x – 2, you were testing to see if x = 2 is a root. You could’ve used synthetic division to do this, because you still get a remainder of 100. And if you plug 2 into f(x) = 2x⁴ – 9x³ – 21x² + 88x + 48, you also get 100.