In word problems, the word of almost always means multiplication. So whenever you see the word of following a fraction, decimal, or percent, you can usually replace it with a times sign.
When you think about it, of means multiplication even when you're not talking about fractions. For example, when you point to an item in a store and say, "I'll take three of those," in a sense you're saying, "I'll take that one multiplied by three."
Renegade grocery shopping: Buying less than they tell you to
When you understand that the word of means multiplication, you have a powerful tool for solving word problems. For instance, you can figure out how much you'll spend if you don't buy food in the quantities listed on the signs. Here's an example:
If beef costs $4 a pound, how much does 5/8 of a pound cost?
Here's what you get if you simply change the of to a multiplication sign:
5/8 x 1 pound of beef
So you know how much beef you're buying. However, you want to know the cost. Because the problem tells you that 1 pound = $4, you can replace 1 pound of beef with $4:
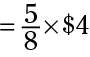
Now you have an expression you can evaluate. Use the rules of multiplying fractions and solve:
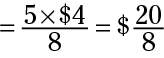
This fraction reduces to $5/2. However, the answer looks weird because dollars are usually expressed in decimals, not fractions. So convert this fraction to a decimal:
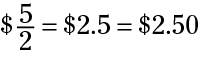
At this point, recognize that $2.5 is more commonly written as $2.50, and you have your answer.
Easy as pie: Working out what's left on your plate
Sometimes when you're sharing something such as a pie, not everyone gets to it at the same time. The eager pie-lovers snatch the first slice, not bothering to divide the pie into equal servings, and the people who were slower, more patient, or just not that hungry cut their own portions from what's left over.
When someone takes a part of the leftovers, you can do a bit of multiplication to see how much of the whole pie that portion represents.
Consider the following example:
Jerry bought a pie and ate 1/5 of it. Then his wife Doreen ate 1/6 of what was left. How much of the total pie was left?
To solve this problem, begin by jotting down what the first sentence tells you:
Jerry = 1/5
Doreen ate part of what was left, so write a word equation that tells you how much of the pie was left after Jerry was finished. He started with a whole pie, so subtract his portion from 1:

Next, Doreen ate 1/6 of this amount. Rewrite the word of as multiplication and solve as follows. This answer tells you how much of the whole pie Doreen ate:
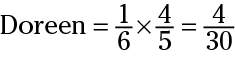
To make the numbers a little smaller before you go on, notice that you can reduce the fraction:
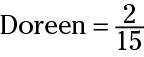
Now you know how much Jerry and Doreen both ate, so you can add these amounts together:

Solve this problem:
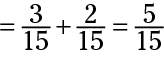
This fraction reduces to 1/3. Now you know that Jerry and Doreen ate 1/3 of the pie, but the problem asks you how much is left. So finish up with some subtraction and write the answer:
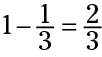
The amount of pie left over was 2/3.





