The first four Pythagorean triple triangles are the favorites of geometry problem-makers. These triples — especially the first and second in the list that follows — pop up all over the place in geometry books. (Note: The first two numbers in each of the triple triangles are the lengths of the legs, and the third, largest number is the length of the hypotenuse).
Here are the first four Pythagorean triple triangles:
The 3-4-5 triangle
The 5-12-13 triangle
The 7-24-25 triangle
The 8-15-17 triangle
You’d do well to memorize these Fab Four so you can quickly recognize them on tests.
Forming irreducible Pythagorean triple triangles
As an alternative to counting sheep some night, you may want to see how many other Pythagorean triple triangles you can come up with.
The first three on the above list follow a pattern. Consider the 5-12-13 triangle, for example. The square of the smaller, odd leg
is the sum of the longer leg and the hypotenuse (12 + 13 = 25). And the longer leg and the hypotenuse are always consecutive numbers. This pattern makes it easy to generate as many more triangles as you want. Here’s what you do:
Take any odd number and square it.

Find the two consecutive numbers that add up to this value.
40 + 41 = 81
You can often just come up with the two numbers off the top of your head, but if you don’t see them right away, just subtract 1 from the result in Step 1 and then divide that answer by 2:
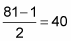
That result and the next larger number are your two numbers.
Write the number you squared and the two numbers from Step 2 in consecutive order to name your triple.
You now have another Pythagorean triple triangle: 9-40-41.
Here are the next few Pythagorean triple triangles that follow this pattern:
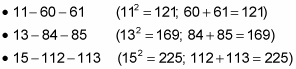
This list is endless — capable of dealing with the worst possible case of insomnia. And note that each triangle on this list is irreducible; that is, it’s not a multiple of some smaller Pythagorean triple triangle (in contrast to the 6-8-10 triangle, for example, which is not irreducible because it’s the 3-4-5 triangle doubled).
When you make a new Pythagorean triple triangle (like the 6-8-10) by blowing up a smaller one (the 3-4-5), you get triangles with the exact same shape. But every irreducible Pythagorean triple triangle has a shape different from all the other irreducible triangles.
Forming further Pythagorean triple triangles
The 8-15-17 triangle is the first Pythagorean triple triangle that doesn’t follow the pattern mentioned previously. Here’s how you generate triples that follow the 8-15-17 pattern:
Take any multiple of 4.
Say you choose 12.
Square half of it.
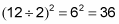
Take the number from Step 1 and the two odd numbers on either side of the result in Step 2 to get a Pythagorean triple triangle.
12-35-37
The next few triples in this infinite set are
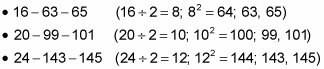
By the way, you can use this process for the other even numbers (the non-multiples of 4) such as 10, 14, 18, and so on. But you get a triangle such as the 10-24-26 triangle, which is the 5-12-13 Pythagorean triple triangle blown up to twice its size, rather than an irreducible, uniquely-shaped triangle.

