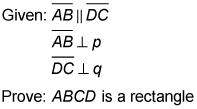When lines and planes are perpendicular and parallel, they have some interesting properties. You can use some of these properties in 3-D proofs that involve 2-D concepts, such as proving that you have a particular quadrilateral or proving that two triangles are similar.
- Three parallel planes: If two planes are parallel to the same plane, then they're parallel to each other.
- Two parallel lines and a plane:
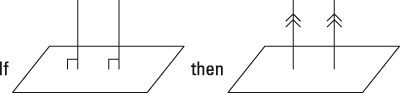
- If two lines are perpendicular to the same plane, then they're parallel to each other.
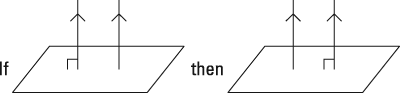
- If a plane is perpendicular to one of two parallel lines, then it's perpendicular to the other.
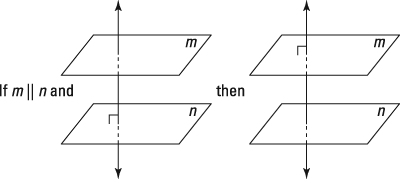
- Two parallel planes and a line:
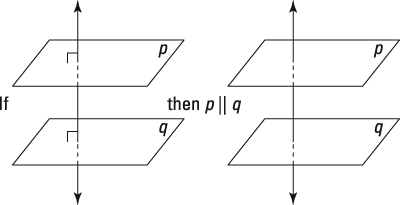
- If two planes are perpendicular to the same line, then they're parallel to each other.
- If a line is perpendicular to one of two parallel planes, then it's perpendicular to the other.
And here's a theorem you need for the example problem that follows.
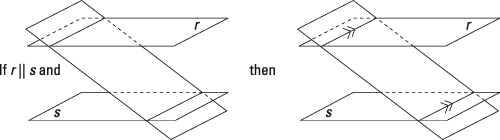
A plane that intersects two parallel planes: If a plane intersects two parallel planes, then the lines of intersection are parallel. Note: Before you use this theorem in a proof, you usually have to show that the plane that cuts the parallel planes is, in fact, a plane.
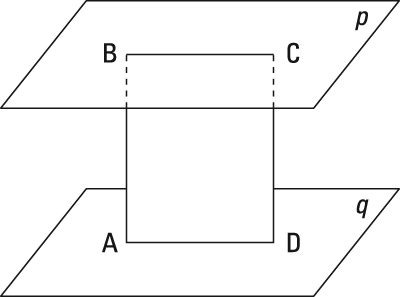
Here's the proof diagram.
Here's the final proof: