A two-column geometry proof is a problem involving a geometric diagram of some sort. You’re told one or more things that are true about the diagram (the givens), and you’re asked to prove that something else is true about the diagram (the prove statement). Every proof proceeds like this:
You begin with one or more of the given facts about the diagram.
You then state something that follows from the given fact or facts; then you state something that follows from that; then, something that follows from that; and so on. Each deduction leads to the next.
You end by making your final deduction — the fact you’re trying to prove.
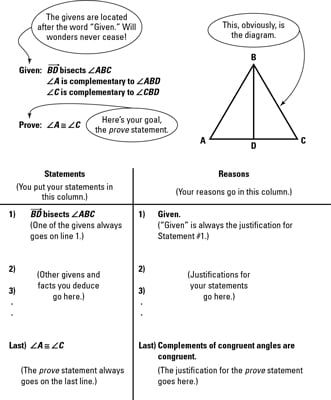
Every standard, two-column geometry proof contains the following elements. The proof mockup in the above figure shows how these elements all fit together.
The diagram: The shape or shapes in the diagram are the subject matter of the proof. Your goal is to prove some fact about the diagram (for example, that two triangles or two angles in the diagram are congruent). The proof diagrams are usually but not always drawn accurately. Don’t forget, however, that you can’t assume that things that look true are true. For instance, just because two angles look congruent doesn’t mean they are.
The givens: The givens are true facts about the diagram that you build upon to reach your goal, the prove statement. You always begin a proof with one of the givens, putting it in line 1 of the statement column.
Most people like to mark the diagram to show the information from the givens. For example, if one of the givens were
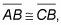
you’d put a little tick mark on both segments so that when you glance at the diagram, the congruence is immediately apparent.
The prove statement: The prove statement is the fact about the diagram that you must establish with your chain of logical deductions. It always goes in the last line of the statement column.
The statement column: In the statement column, you put all the given facts, the facts that you deduce, and in the final line, the prove statement. In this column, you put specific facts about specific geometric objects, such as
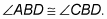
The reason column: In the reason column, you put the justification for each statement that you make. In this column, you write general rules about things in general, such as If an angle is bisected, then it’s divided into two congruent parts. You do not give the names of specific objects.

