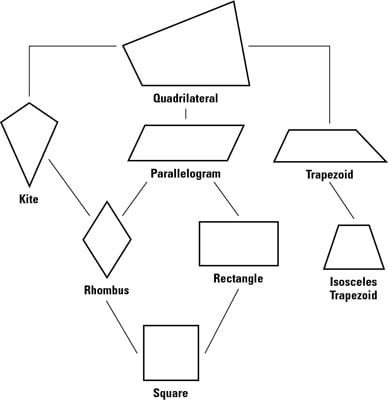
The three-level hierarchy you see with
in the above quadrilateral family tree works just like
A dog is a special type of a mammal, and a Dalmatian is a special type of a dog.
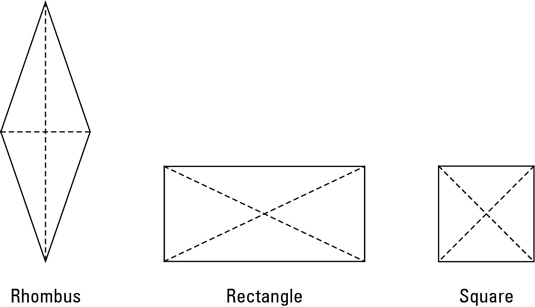
Here are the properties of the rhombus, rectangle, and square. Note that because these three quadrilaterals are all parallelograms, their properties include the parallelogram properties.
-
The rhombus has the following properties:
-
All of the properties of a parallelogram apply (the ones that matter here are parallel sides, opposite angles are congruent, and consecutive angles are supplementary).
-
All sides are congruent by definition.
-
The diagonals bisect the angles.
-
The diagonals are perpendicular bisectors of each other.
-
-
The rectangle has the following properties:
-
All of the properties of a parallelogram apply (the ones that matter here are parallel sides, opposite sides are congruent, and diagonals bisect each other).
-
All angles are right angles by definition.
-
The diagonals are congruent.
-
-
The square has the following properties:
-
All of the properties of a rhombus apply (the ones that matter here are parallel sides, diagonals are perpendicular bisectors of each other, and diagonals bisect the angles).
-
All of the properties of a rectangle apply (the only one that matters here is diagonals are congruent).
-
All sides are congruent by definition.
-
All angles are right angles by definition.
-
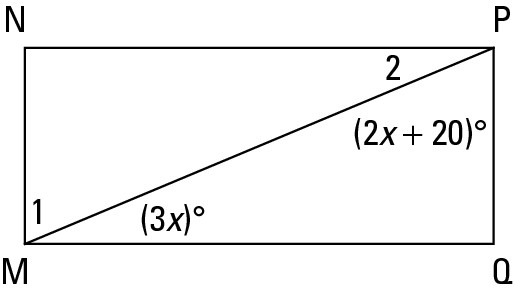
Here’s the solution: MNPQ is a rectangle, so angle Q = 90°. Thus, because there are 180° in a triangle, you can say
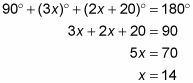
Now plug in 14 for all the x’s.
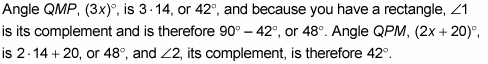
Now find the perimeter of rhombus RHOM.
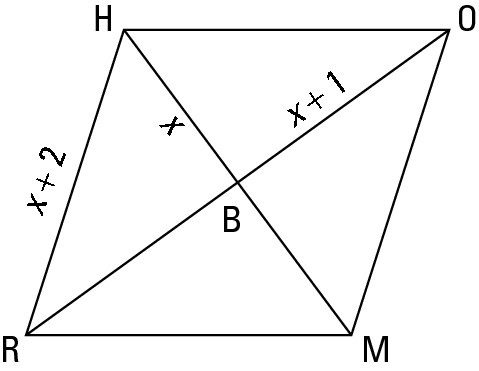
Here’s the solution: All the sides of a rhombus are congruent, so HO equals x + 2. And because the diagonals of a rhombus are perpendicular, triangle HBO is a right triangle. You finish with the Pythagorean Theorem:
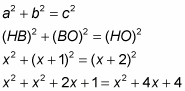
Combine like terms and set equal to zero:
Factor:
(x – 3)(x + 1) = 0
Use Zero Product Property:
x – 3 = 0 or x + 1 = 0
x = 3 or x = –1
You can reject x = –1 because that would result in triangle HBO having legs with lengths of –1 and 0.

