You can prove that triangles are similar using the SSS~ (Side-Side-Side) method. SSS~ states that if the ratios of the three pairs of corresponding sides of two triangles are equal, then the triangles are similar.
The following proof incorporates the Midline Theorem, which states that a segment joining the midpoints of two sides of a triangle is
One-half the length of the third side, and
Parallel to the third side.
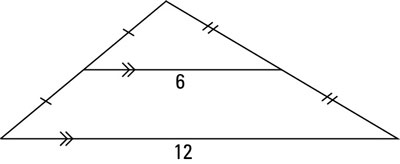
The above figure provides the visual for the theorem.
The first part of the following proof uses the first part of the Midline Theorem and SSS~. The second part of the proof uses the second part of the theorem and proves the triangles similar with AA.
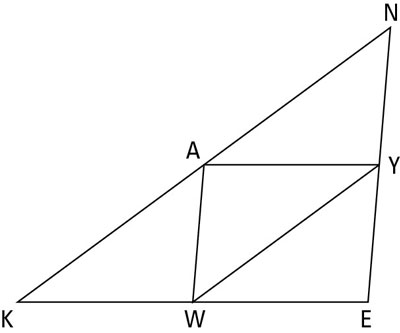

Use the first part of the Midline Theorem to prove that triangle WAY is similar to triangle NEK.
Here’s the solution: The first part of the Midline Theorem says that a segment connecting the midpoints of two sides of a triangle is half the length of the third side. You have three such segments:

Use part two of the Midline Theorem to prove that triangle WAY is similar to triangle NEK.
Solve this one as follows: The second part of the Midline Theorem tells you that a segment connecting the midpoints of two sides of a triangle is parallel to the third side.
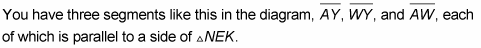
The pairs of parallel segments should make you think about using the parallel-line theorems, which could give you the congruent angles you need to prove the triangles similar with AA (Angle-Angle).
You can use the following parallel-line theorems to prove that angles are congruent. That is, if two parallel lines are cut by a transversal, then . . .
Corresponding angles are congruent.
Alternate interior angles are congruent.
Alternate exterior angles are congruent.


