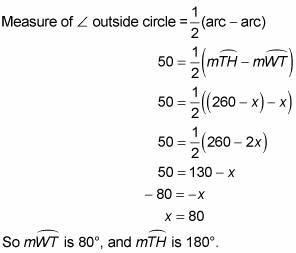An angle that intersects a circle can have its vertex inside, on, or outside the circle. This article discusses the three types of angles that have their vertex outside a circle: secant-secant angles, secant-tangent angles, and tangent-tangent angles. A tangent is a line that touches a circle at a single point; a secant is a line that intersects a circle at two points.
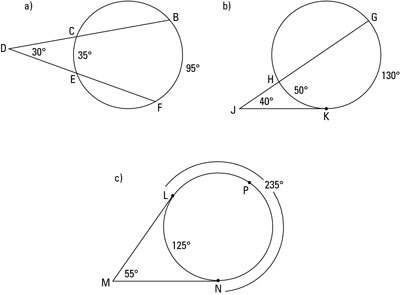
So here are the three types of angles that have their vertex outside a circle:
-
Secant-secant angle: A secant-secant angle, like angle BDF in the above figure on the top left, is an angle whose vertex lies outside a circle and whose sides are two secants of the circle.
-
Secant-tangent angle: A secant-tangent angle, like angle GJK in the above figure on the top right, is an angle whose vertex lies outside a circle and whose sides are a secant and a tangent of the circle.
-
Tangent-tangent angle: A tangent-tangent angle, like angle LMN in the above figure on the bottom, is an angle whose vertex lies outside a circle and whose sides are two tangents of the circle.
Measure of an angle outside a circle: The measure of a secant-secant angle, a secant-tangent angle, or a tangent-tangent angle is one-half the difference of the measures of the intercepted arcs. For example, in the above figure,
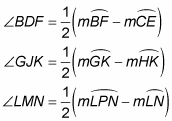
Note that you subtract the smaller arc from the larger (if you get a negative answer, you know you subtracted in the wrong order).
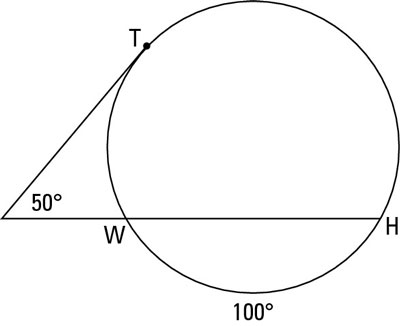
Now, using the above figure, solve this problem with the angle-outside-a-circle formula:

Plug these expressions into the formula, and you’re home free: