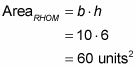Here’s a rhombus area problem involving triangles and ratios: Find the area of rhombus RHOM given that MB is 6 and that the ratio of RB to BH is 4 : 1, as shown in the following figure.
This problem’s a bit gnarly. You might feel that you’re not given enough information to solve it or that you just don’t know how to begin. If you ever feel this way when you’re in the middle of a math problem, here’s a great tip for you:
If you get stuck when doing a geometry problem — or any kind of math problem, for that matter — do something, anything! Begin anywhere you can: Use the given information or any ideas you have (try simple ideas before more-advanced ones) and write something down. Maybe draw a diagram if you don’t have one. Put something down on paper. This tip is surprisingly effective. One idea may trigger another, and before you know it, you’ve solved the problem.
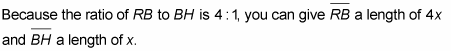
Then, because all sides of a rhombus are congruent, RM must equal RH, which is 4x + x, or 5x.

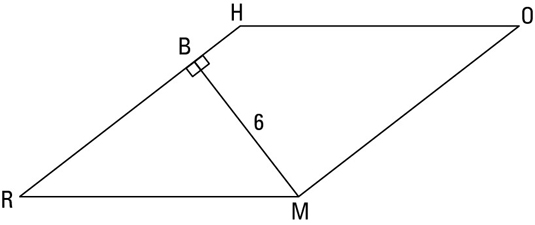
Because the lengths of the sides must be positive, you reject the answer x = –2. The length of the base, segment RH, is thus 5(2), or 10. (Triangle RBM is a 3-4-5 triangle blown up by a factor of 2.) Now use the parallelogram/rhombus area formula: