To put angles on the coordinate plane, essentially all you do is look at the trig ratios in terms of x and y values rather than opposite, adjacent, and hypotenuse. Redefining these ratios to fit the coordinate plane (sometimes called the point-in-the-plane definition) makes visualizing these easier. Some of the angles, for instance, are larger than 180 degrees, but you can make a right triangle by using a point and the x-axis. You then use the new ratios to find missing sides of right triangles and/or trig function values of angles.
When a point (x, y) exists on a coordinate plane, you can calculate all the trig functions of the angle between the positive x-axis and the line segment from the origin to the point (x,y) by following the steps below (use the following figure):
Locate the point on the coordinate plane and connect it to the origin, using a straight line.
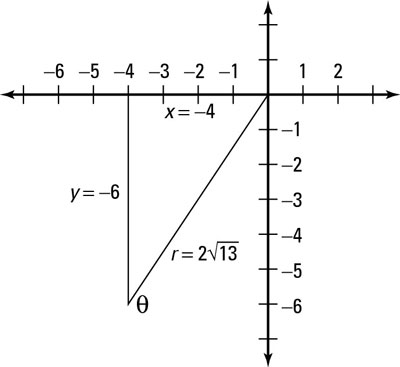
Say, for example, that you're asked to evaluate all six trig functions of the angle between the positive x-axis and the line segment joining the origin to the point in the plane (–4, –6). The line segment moving from this point to the origin is your hypotenuse and is now called the radius r (as you see in the figure).
Draw a perpendicular line connecting the given point to the x-axis, creating a right triangle.
The legs of the right triangle are –4 and –6. Don't let the negative signs scare you; the lengths of the sides are still 4 and 6. The negative signs just reveal the location of that point on the coordinate plane.
Find the length of the hypotenuse r by using the distance formula or the Pythagorean theorem.
The distance you want to find is the length of r from Step 1. Using the distance formula between (x, y) and the origin (0, 0), you get
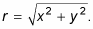
Remember that this equation implies the principal or positive root only, so the hypotenuse for these point-in-the-plane triangles is always positive.
For this example, you get
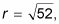
which simplifies to
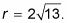
Check out what the triangle looks like in the figure.
Evaluate the trig function values, using their alternate definitions.
With the labels from the figure, you get the following formulas:

Substitute the numbers from the example in the figure to pinpoint the trig values:
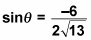
Simplify first:
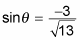
Then rationalize the denominator:
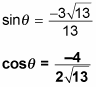
Simplify first:
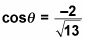
Then rationalize:
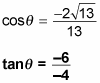
This answer simplifies to 3/2.

Notice that the rules of trig functions and their reciprocals still apply. For example, if you know
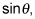
you automatically know
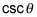
because they're reciprocals.
When the point you're given is a point on one of the axes, you can still find all the trig function values of the angle formed with the positive x-axis. For instance, if the point is on the x-axis, the leg adjacent to the angle theta and the radius have the same absolute value (because the cosine can be negative but the radius can't). Therefore, if the point is on the positive x-axis, the cosine of theta is 1 and the sine of theta is 0; if the point is on the negative x-axis, the cosine of theta is –1 and the sine of theta will still be 0. Similarly, if the point is on the y-axis, the leg opposite the angle theta and the radius are of the same absolute value. Therefore, if the point is on the positive y-axis, the sine of theta will be 1, and the cosine will be 0; if the point is on the negative y-axis, the sine of theta will be –1 and the cosine will still be 0.

