Understanding the Properties and Identities of Logs

You need to know several properties of logs in order to solve equations that contain them. Each of these properties applies to any base, including the common and natural logs:

• log_b 1 = 0

  If you change back to an exponential function, b⁰ = 1 no matter what the base is. So, it makes sense that log_b 1 = 0.

• log_b x exists only when x is greater than or equal to 0

  

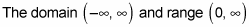
  of the original exponential parent function switch places in any inverse function. Therefore, any logarithm parent function has the domain of

  

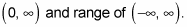
• log_bb^x = x

  You can change this logarithmic property into an exponential property by using the snail rule: b^x = b^x. (The figure gives you an illustration of this property.)

  

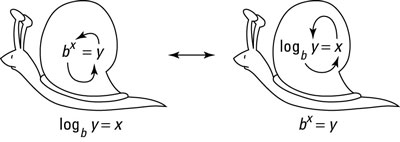
  No matter what value you put in for b, this equation always works. Also note log_b b = 1 no matter what the base is (because it’s really just log_b b¹).

  The fact that you can use any base you want in this equation illustrates how this property works for common and natural logs: log 10^x = x and ln e^x = x.

• b^log_b^x = x

  You can change this equation back to a log to confirm that it works: log_b x = log_b x.

• log_b x + log_b y = log_b(xy)

  According to this rule, called the product rule, log₄ 10 + log₄ 2 = log₄ 20.

• log_bx + log_by = log_b(x/y)

  According to this rule, called the quotient rule,

  

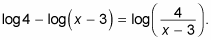
• log_bx^y = (y)(log_bx)

  According to this rule, called the power rule,

  

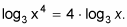
Remember to keep the properties of logs straight so you don’t get confused and make a critical mistake. The following list highlights many of the mistakes that people make when it comes to working with logs:

• Misusing the product rule:

  

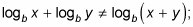
  this equals log_b(xy). You can’t add two logs inside of one. Similarly,

  

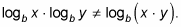
• Misusing the quotient rule:

  

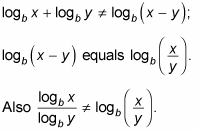
  This error messes up the change of base formula (which is described in the following section).

• Misusing the power rule:

  

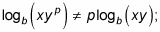
  this is because the power is on the second variable only. If the formula was written as log_b(xy)^p, it would equal plog_b(xy).

  Note: Watch what those exponents are doing. You should split up the multiplication from log_b(xy^p) first by using the product rule: log_b x + log_b y^p. Only then can you apply the power rule to get log_b x + plog_b y.

How to change a log’s base

Calculators usually come equipped with only common log or natural log buttons, so you must know what to do when a log has a base your calculator can’t recognize, such as log₅ 2; the base is 5 in this case. In these situations, you must use the change of base formula to change the base to either base 10 or base e (the decision depends on your personal preference) in order to use the buttons that your calculator does have.

Following is the change of base formula:

You can make the new base anything you want (5, 30, or even 3,000) by using the change of base formula, but remember that your goal is to be able to utilize your calculator by using either base 10 or base e to simplify the process. For instance, if you decide that you want to use the common log (base 10) in the change of base formula, you find that

However, if you’re a fan of natural logs, you can go this route:

which is still 1.465.