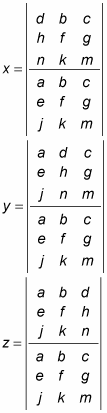Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonIf your pre-calculus teacher asks you to solve a system of equations, you can impress him or her by using Cramer's rule instead of using a graphing calculator.
Cramer's rule says that if the determinant of a coefficient matrix |A| is not 0, then the solutions to a system of linear equations can be found as follows:
If the matrix describing the system of equations looks like this:
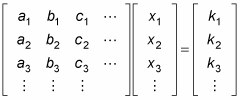
Then

and so on until you have solved for all the variables. In other words, the solution components are readily obtained by computing the appropriate ratios of determinants of a family of matrices. Notice that the denominator of these components is the determinant of the coefficient matrix.
This rule is helpful when the systems are very small or when you can use a graphing calculator to determine the determinants because it helps you find the solutions with minimal places to get mixed up. To use it, you simply find the determinant of the coefficient matrix.
The determinant of a 2-x-2 matrix like this one:
is defined to be ad – bc. The determinant of a 3-x-3 matrix is a bit more complicated. If the matrix is
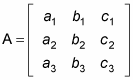
then you can find the determinant by following these steps:
Rewrite the first two columns immediately after the third column.
Draw three diagonal lines from the upper left to the lower right and three diagonal lines from the lower left to the upper right, as shown in this figure.
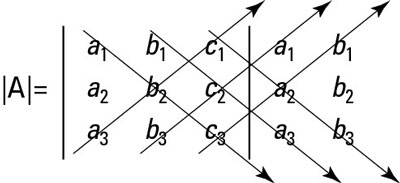 How to find the determinant of a 3-x-3 matrix.
How to find the determinant of a 3-x-3 matrix.Multiply down the three diagonals from left to right and then add these products. Multiply up the other three from left to right and add these products. Then subtract the second sum from the first sum.
The determinant of the 3-x-3 matrix is:
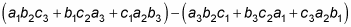
To find the determinant of this 3-x-3 matrix:

you use a process known as using diagonals, which you can see in this figure.
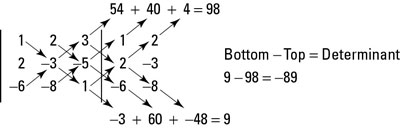
This example provides a shortcut to finding the determinant of a 3-x-3 matrix. For 4 x 4 and larger matrices, the methods used here are not valid.
After you find the determinant of the coefficient matrix (either by hand or with a technological device), replace the first column of the coefficient matrix with the answer matrix from the other side of the equal sign and find the determinant of that new matrix. Then replace the second column of the coefficient matrix with the answer matrix and find the determinant of that matrix. Continue this process until you have replaced each column and found each new determinant. The values of the respective variables are equal to the determinant of the new matrix (when you replaced the respective column) divided by the determinant of the coefficient matrix.
You can't use Cramer's rule when the matrix isn't square or when the determinant of the coefficient matrix is 0, because you can't divide by 0. Cramer's rule is most useful for a 2-x-2 or higher system of linear equations.
To solve a 3-x-3 system of equations such as
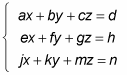
using Cramer's rule, you set up the variables as follows: