Say you’re filling up your swimming pool and you know how fast water is coming out of your hose, and you want to calculate how fast the water level in the pool is rising. You know one rate (how fast the water is being poured in), and you want to determine another rate (how fast the water level is rising). These rates are called related rates because one depends on the other — the faster the water is poured in, the faster the water level will rise. In a typical related rates problem, the rate or rates you’re given are unchanging, but the rate you have to figure out is changing with time. You have to determine this rate at one particular point in time.
In this example, one car leaves an intersection traveling north at 50 mph, and another is driving west toward the intersection at 40 mph. At one point, the north-bound car is 3/10 mile north of the intersection, and the west-bound car is 4/10 mile east of the intersection. At this point, how fast is the distance between the cars changing?
Draw a diagram.
Label the diagram with any unchanging numbers and assign variables to any changing things. (Note that the numbers 0.3 and 0.4 are in parentheses to indicate that they are not unchanging values.)
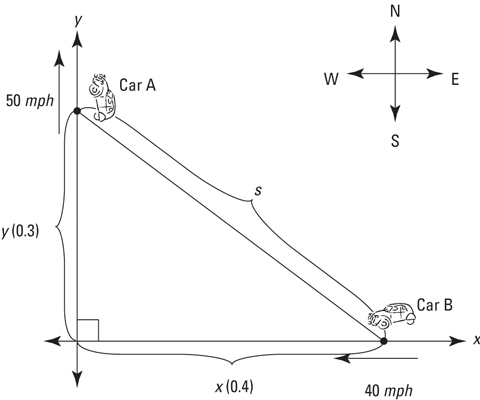
List all given rates and the unknown rate.

Write the formula that relates the variables in the problem: x, y, and s.
There’s a right triangle in the diagram, so you use the Pythagorean Theorem:
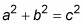
For this problem, x and y are the legs of the right triangle, and s is the hypotenuse, so
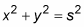
Differentiate with respect to t.

Use the Pythagorean Theorem again to solve for s.
x = 0.4
y = 0.3

You can reject the negative answer because s obviously has a positive length. So s = 0.5.
Now you’ve got everything you need to substitute into the differentiation result and solve for ds/dt.
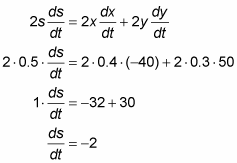
This negative answer means that the distance, s, is decreasing. Thus, when car A is 3 blocks north of the intersection and car B is 4 blocks east of the intersection, the distance between them is decreasing at a rate of 2 mph.

