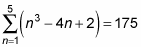Summation notation is a useful way to represent the partial sum of a sequence. The sum of the first k terms of an arithmetic sequence is referred to as the kth partial sum. They're called partial sums because you're only able to find the sum of a certain number of terms — no infinite series here! You may use partial sums when you want to find the area under a curve (graph) between two certain values of x. Although finding the entire area under the graph isn't always possible (because it could be infinite if the curve goes on forever), you can find the area underneath a piece of it.
Don't let the use of the k variable confuse you. Instead of k, your book may use n and call it an nth partial sum. Remember that a variable just stands in for an unknown, so it really can be any variable you want — even a Greek variable. But most books use k to represent the number of terms in a series and n for the number of terms in a sequence.
The notation of the kth partial sum of a sequence is as follows:
You read this equation as "the kth partial sum of an is . . ." where n = 1 is the lower limit of the sum and k is the upper limit of the sum. To find the kth partial sum, you begin by plugging the lower limit into the general formula and continue in order, plugging in integers until you reach the upper limit of the sum. At that point, you simply add all the terms to find the sum.
To find the fifth partial sum of an = n3 – 4n + 2, for example, follow these steps:
Plug all values of n (starting with 1 and ending with k) into the formula.
Because you want to find the fifth partial sum, plug in 1, 2, 3, 4, and 5:
a1 = (1)3 – 4(1) + 2 = 1 – 4 + 2 = –1
a2 = (2)3 – 4(2) + 2 = 8 – 8 + 2 = 2
a3 = (3)3 – 4(3) + 2 = 27 – 12 + 2 = 17
a4 = (4)3 – 4(4) + 2 = 64 – 16 + 2 = 50
a5 = (5)3 – 4(5) + 2 = 125 – 20 + 2 = 107
Add all the values from a1 to ak to find the sum.
This step gives you
–1 + 2 + 17 + 50 + 107 = 175
Rewrite the final answer, using summation notation.