When you're asked to simplify an expression involving cosecant, secant, or cotangent, you change the expression to functions that involve sine, cosine, or tangent, respectively. When you change functions in this manner, you're using reciprocal identities. (Technically, the identities are trig functions that just happen to be considered identities as well because they help you simplify expressions.) You use reciprocal identities so that you can cancel functions and simplify the problem.
The following list presents these reciprocal identities:
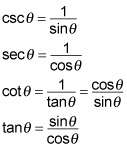
Every trig ratio can be written as a combination of sines and/or cosines, so changing all the functions in an equation to sines and cosines is the simplifying strategy that works most often. Always try to do this step first and then look to see if things cancel and simplify. Also, dealing with sines and cosines is usually easier if you're looking for a common denominator for fractions. From there, you can use what you know about fractions to simplify as much as you can.
Look for opportunities to use reciprocal identities whenever the problem you're given contains secant, cosecant, or cotangent. All these functions can be written in terms of sine and cosine, and sines and cosines are always the best place to start. For example, you can use reciprocal identities to simplify this expression:
Follow these steps:
Change all the functions into versions of the sine and cosine functions.
Because this problem involves a cosecant and a cotangent, you use the reciprocal identities to change

This process gives you
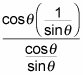
Break up the complex fraction by rewriting the division bar that's present in the original problem as
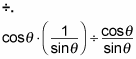
Invert the last fraction and multiply.
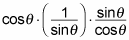
Cancel the functions to simplify.
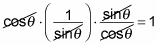
The sines and cosines cancel, and you end up getting 1 as your answer.

