You can measure the volume of any irregular-shaped solid with a cross section that’s a function of x. In some cases, these solids are harder to describe than they are to measure. For example, have a look at this figure.
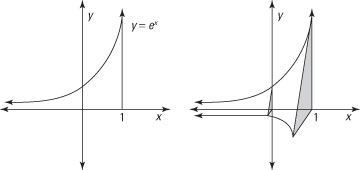
The solid in the figure consists of two exponential curves — one described by the equation y = ex and the other described by placing the same curve directly in front of the x-axis — joined by straight lines. The other sides of the solid are bounded planes slicing perpendicularly in a variety of directions.
Notice that when you slice this solid perpendicular with the x-axis, its cross section is always an isosceles right triangle. This is an easy shape to measure, so the slicing method works nicely to measure the volume of this solid. Here are the steps:
Find an expression that represents the area of a random cross section of the solid.
The triangle on the y-axis has a height and base of 1 — that is, e0. And the triangle on the line x = 1 has a height and base of e1, which is e. In general, the height and base of any cross section triangle is ex.
So here’s how to use the formula for the area of a triangle to find the area of a cross section in terms of x:

Use this expression to build a definite integral that represents the volume of the solid.
Now that you know how to measure the area of a cross section, integrate to add all the cross sections from x = 0 to x = 1:

Evaluate this integral to find the volume.






