After you calculate all the asymptotes and the x- and y-intercepts for a rational function, you have all the information you need to start graphing the function. In any rational function where the denominator has a greater degree, as values of x get infinitely large, the fraction gets infinitely smaller until it approaches zero (this process is called a limit).
Rational functions are really just fractions. If you look at several fractions where the numerator stays the same but the denominator gets bigger, the whole fraction gets smaller. For instance, look at 1/2, 1/20, 1/200, and 1/2,000.
When the denominator has the greater degree, you begin by graphing the information that you know for f(x):
The figure shows all the parts of the graph:
Draw the vertical asymptote(s).
Whenever you graph asymptotes, be sure to use dotted lines, not solid lines, because the asymptotes aren’t part of the rational function.
 The graph of f(x) with asymptotes and intercepts filled in.
The graph of f(x) with asymptotes and intercepts filled in.For f(x), you find that the vertical asymptotes are x = –7 and x = 3, so draw two dotted vertical lines, one at x = –7 and another at x = 3.
Draw the horizontal asymptote(s).
Continuing with the example, the horizontal asymptote is y = 0 — or the x-axis.
Plot the x-intercept(s) and the y-intercept(s).
The y-intercept is y = 1/21, and the x-intercept is x = 1/3.
Now you fill in the blanks by plotting outputs of test values. The vertical asymptotes divide the graph and the domain of f(x) into three intervals:
For each of these three intervals, you must pick at least one test value and plug it into the original rational function; this test determines whether the graph on that interval is above or below the horizontal asymptote (the x-axis). Follow these steps:
Test a value in the first interval.
In this example, the first interval is
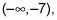
so you can choose any number you want as long as it’s less than –7. For example, if you choose x = –8, you then evaluate
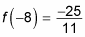
This negative value tells you that the function is under the horizontal asymptote on the first interval only.
Test a value in the second interval.
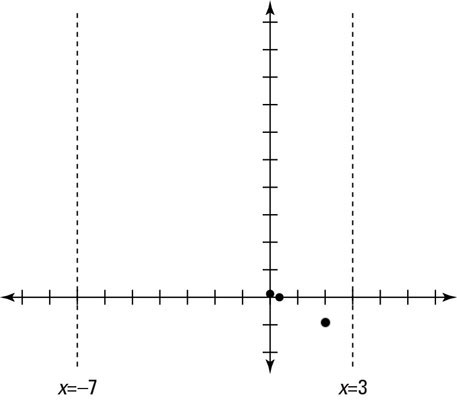
If you look at the second interval (–7, 3) in the figure, you’ll realize that you already have two test points located in it. The y-intercept has a positive value, which tells you that the graph is above the horizontal asymptote for that part of the graph.
Now here comes the curve ball: It stands to reason that a graph should never cross an asymptote; it should just get closer and closer to it. In this case, there’s an x-intercept, which means that the graph actually crosses its own horizontal asymptote. The graph becomes negative for the rest of this interval.
Vertical asymptotes are the only asymptotes that are never crossed. A horizontal asymptote actually tells you what value the graph is approaching for infinitely large positive or negative values of x.
Test a value in the third interval.
For the third interval,
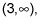
let’s say you use the test value of 4 (you can use any number greater than 3) to determine the location of the graph on the interval. You get f(4) = 1, which tells you that the graph is above the horizontal asymptote for this last interval.
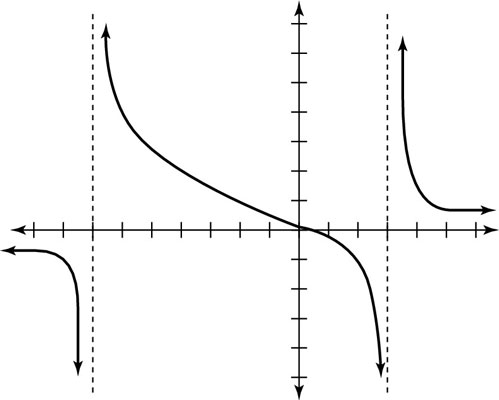
Knowing a test value in each interval, you can plot the graph by starting at a test value point and moving from there toward both the horizontal and vertical asymptotes. This figure shows the complete graph of f(x).

