The double-angle formula for tangent is used less often than the double-angle formulas for sine or cosine; however, you shouldn't overlook it just because it isn't as popular as its cooler counterparts!
The double-angle formula for tangent is derived by rewriting tan 2x as tan(x + x) and then applying the sum formula. However, the double angle formula for tangent is much more complicated here because it involves fractions. So you should just memorize the formula.
The double-angle identity for tangent is
When solving equations for tangent, remember that the period for the tangent function is pi. This detail is important — especially when you have to deal with more than one angle in an equation — because you usually need to find all the solutions on the interval [0, 2pi). Double-angle equations have twice as many solutions in that interval as single-angle equations do.
Follow these steps to find the solutions for 2 tan 2x + 2 = 0 on the interval [0, 2pi):
Isolate the trig function.
Subtract 2 from both sides to get 2 tan 2x = –2. Divide both sides of the equation by 2 next: tan 2x = –1.
Solve for the double-angle by using the unit circle.
On the unit circle, the tangent is negative in the second and fourth quadrants. Moreover, the tangent is –1 at
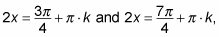
where k is an integer.
Note: You have to add pi multiplied by k to each solution to find all the solutions of the equation.
Isolate the variable.
Divide both sides of the equation by 2 to find x. (Remember that you have to divide both the angle and the period by 2.) This step gives you

Find all the solutions on the required interval.
Continue adding pi/2 to (3pi)/8 and (7pi)/8 until you obtain all the solutions to the equation that lie in the interval [0,2pi). Of course, first you must find a common denominator — in this case, 8. Beginning with (3pi)/8:
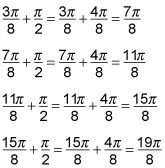
However, (19pi)/8 is not in the interval [0,2pi). So you stop here and this solution is not considered. Hence the four solutions so far are (3pi)/8, (7pi)/8, (11pi)/8, and (15pi)/8. You must now follow the same process as above beginning with (7pi)/8. You will soon observe that following this process beginning with (7pi)/8 will not get you any additional solutions. Hence the four solutions listed are all of the solutions in the interval [0, 2pi).

