Knowing how volume is measured without calculus pays off big-time when you step into the calculus arena. This is strictly no-brainer stuff — some basic, solid geometry that you probably know already.
One of the simplest solids to find the volume of is a prism. A prism is a solid that has all congruent cross sections in the shape of a polygon. That is, no matter how you slice a prism parallel to its base, its cross section is the same shape and area as the base itself.
The formula for the volume of a prism is simply the area of the base times the height:
V = Ab · h
So if you have a triangular prism with a height of 3 inches and a base area of 2 square inches, its volume is 6 cubic inches.
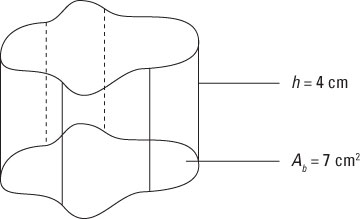
This formula also works for cylinders — which are sort of prisms with a circular base — and generally any solid that has congruent cross sections. For example, the odd-looking solid in the figure fits the bill nicely. In this case, you’re given the information that the area of the base is 7 cm2 and the height is 4 cm, so the volume of this solid is 28 cm3.
Finding the volume of a solid with congruent cross sections is always simple as long as you know two things:
The area of the base — that is, the area of any cross section
The height of the solid





