The three-dimensional (3-D) Cartesian coordinate system (also called 3-D rectangular coordinates) is the natural extension of the 2-D Cartesian graph. The key difference is the addition of a third axis, the z-axis, extending perpendicularly through the origin.
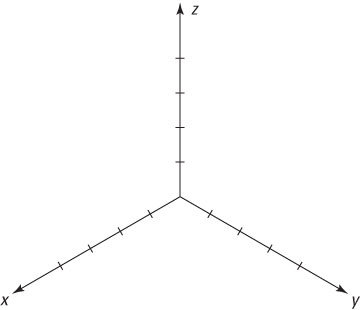
Drawing a 3-D graph in two dimensions is kind of tricky. To get a better sense about how to think in 3-D, hold up the figure where you can compare it with the interior corner of a room (not a round room!). Note the following:
The x-axis corresponds to where the left-hand wall meets the floor.
The y-axis corresponds to where the right-hand wall meets the floor.
The z-axis corresponds to where the two walls meet.
Just as the 2-D Cartesian graph is divided into four quadrants, the 3-D graph is divided into eight octants. From your perspective as you look at the graph, you’re standing inside the first octant, where all values of x, y, and z are positive.
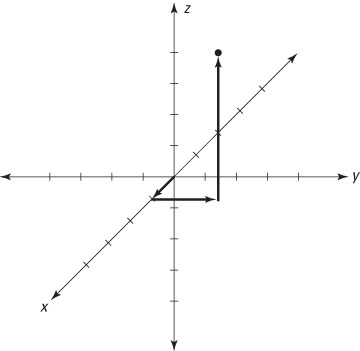
The figure above shows the complete 3-D Cartesian system with the point (1, 2, 5) plotted. In similarity with regular Cartesian coordinates, you plot this point by counting 1 unit in the positive x direction, and then 2 units in the positive y direction, and finally 5 units in the positive z direction.

