Connecting a Series with Its Two Related Sequences

Every series has two related sequences: a defining sequence and a sequence of partial sums. The distinction between a sequence and a series is as follows:

• A sequence is a list of numbers separated by commas (for example: 1, 2, 3, ...).

• A series is a sum of numbers separated by plus signs (for example: 1 + 2 + 3 + ...).

When you see how a series and its two related sequences are distinct but also related, you gain a clearer understanding of how series work.

A series and its defining sequence

The first sequence related to a series is simply the sequence that defines the series in the first place. For example, here are three series written in both sigma notation and expanded notation, each paired with its defining sequence:

When a sequence {a_n} is already defined, you can use the notation ∑ a_n to refer to the related series starting at n = 1. For example, when

Understanding the distinction between a series and the sequence that defines it is important for two reasons. First, and most basic, you don’t want to get the concepts of sequences and series confused. But second, the sequence that defines a series can provide important information about the series.

A series and its sequences of partial sums

You can learn a lot about a series by finding the partial sums of its first few terms. For example, here’s a series that you’ve seen before:

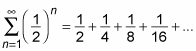
And here are the first four partial sums of this series:

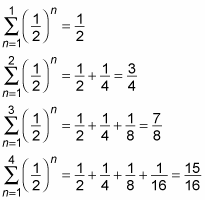
You can turn the partial sums for this series into a sequence as follows:

In general, every series ∑ a_n has a related sequence of partial sums {S_n}. For example, here are a few such pairings:

Remember that every series and its related sequence of partial sums are either both convergent or both divergent. Moreover, if they’re both convergent, both converge to the same number.

This rule should come as no big surprise. After all, a sequence of partial sums simply gives you a running total of where a series is going. Still, this rule can be helpful. For example, suppose that you want to know whether the following sequence is convergent or divergent:

What the heck is this sequence, anyway? Upon deeper examination, however, you discover that it’s the sequence of partial sums for a very simple series:

This series, called the harmonic series, is divergent, so you can conclude that its sequence of partial sums also diverges.