When comparing data samples from different populations, two of the most popular measures of association are covariance and correlation. Covariance and correlation show that variables can have a positive relationship, a negative relationship, or no relationship at all.
A sample is a randomly chosen selection of elements from an underlying population.
Sample covariance measures the strength and the direction of the relationship between the elements of two samples, and the sample correlation is derived from the covariance. The sample covariance between two variables, X and Y, is
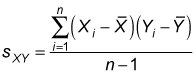
Here's what each element in this equation means:
sXY = the sample covariance between variables X and Y (the two subscripts indicate that this is the sample covariance, not the sample standard deviation).

n = the number of elements in both samples.
i = an index that assigns a number to each sample element, ranging from 1 to n.
Xi = a single element in the sample for X.
Yi = a single element in the sample for Y.
The sample covariance may have any positive or negative value.
You calculate the sample correlation (also known as the sample correlation coefficient) between X and Y directly from the sample covariance with the following formula:
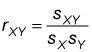
The key terms in this formula are
rXY = sample correlation between X and Y
sXY = sample covariance between X and Y
sX = sample standard deviation of X
sY = sample standard deviation of Y
The formula used to compute the sample correlation coefficient ensures that its value ranges between –1 and 1.
For example, suppose you take a sample of stock returns from the Excelsior Corporation and the Adirondack Corporation from the years 2008 to 2012, as shown here:
| Year | Excelsior Corp. Annual Return (percent) (X) | Adirondack Corp. Annual Return (percent) (Y) |
|---|---|---|
| 2008 | 1 | 3 |
| 2009 | –2 | 2 |
| 2010 | 3 | 4 |
| 2011 | 0 | 6 |
| 2012 | 3 | 0 |
What are the covariance and correlation between the stock returns? To figure that out, you first have to find the mean of each sample. In this example, X represents the returns to Excelsior and Y represents the returns to Adirondack.
The sample mean of X is
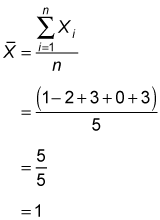
You obtain the sample mean by summing all the elements of the sample and then dividing by the sample size. In this case, the sample elements sum to 5 and the sample size is 5. Dividing these numbers gives a sample mean of 1.
The sample mean of Y is
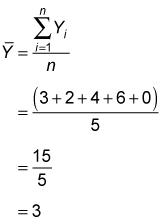
This table shows the remaining calculations for the sample covariance:

In the table, the
column represents the differences between each return to Excelsior in the sample and the sample mean; similarly, the
column represents the same calculations for Adirondack. The entries in the
column equal the product of the entries in the previous two columns. The sum of the
column gives the numerator in the sample covariance formula:
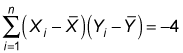
The denominator equals the sample size minus one, which is 5 – 1 = 4. (Both samples have five elements, n = 5.) Therefore, the sample covariance equals
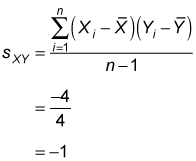
To calculate the sample correlation coefficient, divide the sample covariance by the product of the sample standard deviation of X and the sample standard deviation of Y:
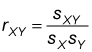
You find the sample standard deviation of X by computing the sample variance of X and then taking the square root of the result. The table shows the calculations for the sample variance of X.

In the table, the
column represents the differences between each return to Excelsior in the sample and the sample mean; the
column represents the squared difference between each return to Excelsior and the sample mean. The sum of the
column gives the numerator in the sample variance formula. You divide this number by the sample size minus one (5 – 1 = 4) to get the sample variance of X:
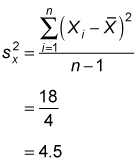
The sample standard deviation of X is the square root of 4.5, or
The table shows the calculations for the sample variance of Y.

Based on the calculations in the table, the sample variance of Y equals
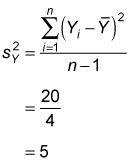
The sample standard deviation of Y equals the square root of 5, or
Substituting these values into the sample correlation formula gives you
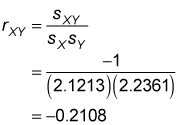
The negative result shows that there's a weak negative correlation between the stock returns of Excelsior and Adirondack. If two variables are perfectly negatively correlated (they always move in opposite directions), their correlation will be –1. If two variables are independent (unrelated to each other), their correlation will be 0. The correlation between the returns to Excelsior and Adirondack stock is a –0.2108, which indicates that the two variables show a slight tendency to move in opposite directions.

