When you use a small sample to test a hypothesis about a population mean, you take the resulting critical value or values from the Student's t-distribution. For a two-tailed test, the critical value is

and n represents the sample size.
| Degrees of Freedom | t0.10 | t0.05 | t0.025 | t0.01 | t0.005 |
|---|---|---|---|---|---|
| 6 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 |
| 7 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 |
| 8 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 |
| 9 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 11 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 |
| 12 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 |
| 13 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 |
| 14 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 |
| 15 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 |
The number of degrees of freedom used with the t-distribution depends on the particular application. For testing hypotheses about the population mean, the appropriate number of degrees of freedom is one less than the sample size (that is, n – 1).
The critical value or values are used to locate the areas under the curve of a distribution that are too extreme to be consistent with the null hypothesis. For a two-tailed test, the value of the level of significance
is split in half; the area in the right tail equals
and the area in the left tail equals
As an example of a two-tailed test, suppose the level of significance is 0.05 and the sample size is 10; then you get a positive and a negative critical value:
You can get the value of the positive critical value
directly from the Student's t-distribution table.
In this case, you find the positive critical value t90.025 at the intersection of the row representing 9 degrees in the Degrees of Freedom column and the t0.025 column. The positive critical value is 2.262; therefore, the negative critical value is –2.262. You represent these two values like so:
You represent them graphically as shown here.
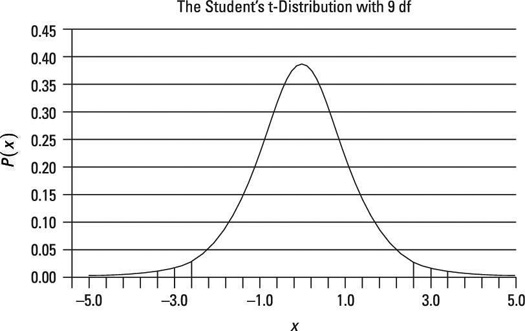
The shaded region in the two tails represents the rejection region; if the test statistic falls in either tail, the null hypothesis will be rejected.

