The difference quotient shows up in most high school Algebra II classes as an exercise you do after your instructor shows you the composition of functions. You perform this exercise because the difference quotient is the basis of the definition of the derivative.
The difference quotient allows you to find the derivative, which allows you to be successful in calculus (because everyone wants to be successful in calculus, of course). So, where does the composition of functions come in? With the difference quotient, you do the composition of some designated function f (x) and the function
depending on what calculus book you use.
The difference quotient for the function f is
Yes, you have to memorize it.
Now, for an example, perform the difference quotient on the function, f (x) = x2 – 3x – 4:
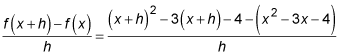
Notice that you find the expression for f (x + h) by putting x + h in for every x in the function — x + h is the input variable. Now, continuing on with the simplification:
Did you notice that x2, 3x, and 4 all appear in the numerator with their opposites? That's why they disappear with the simplification. Now, to finish:
Now, this may not look like much to you, but you've created a wonderful result. You're one step away from finding the derivative.





