Combinations are another way of counting items. This time, you select some items from a larger group, but you don’t care what order they come in. For instance, if you select 6 lottery numbers from a listing of 54, which number was chosen first or second or third doesn’t matter — just that you chose them.
You can find the number of combinations or ways to choose r elements from a set containing n elements with the formula
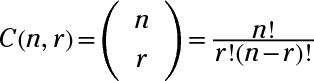
The two different notations and nCr are commonly used to indicate that you’re finding the number of combinations. Notice that this formula looks very much like the formula for permutations. The extra factor in the denominator makes the total number smaller.
Sample questions
Find the number of ways (combinations) of selecting 6 lottery numbers from 54 choices.
25,827,165. (At $1 per entry, no wonder your chances are so slim.) Here’s the math:

Each of the factors in the denominator divides into a factor in the numerator, so the result is always a whole number.
At a restaurant, the specialty platter includes a choice of any two of the five entrees and any three of the ten sides. How many different platters are possible?
1,200. Use C(5, 2) to choose the entrees and C(10, 3) to choose the sides. Then multiply the two results together:

You find that 1,200 different platters are possible.
Practice questions
You can invite 9 of your 20 best friends to your birthday party. How many different combinations of friends are possible?
A lottery has you choose 8 numbers from 60. How many different winning combinations are possible?
You’re selecting a committee of eight. Four are to be chosen from a group of 10 men, and 4 are to be chosen from a group of 20 women. How many different committees can you have?
You’re going to sample 5 fruit cups out of the total shipment of 400. If those 5 cups are okay, then you can assume that the whole shipment is okay. How many different ways can you choose 5 fruit cups out of 400?
Following are answers to the practice questions:
The answer is 167,960.
This is a combination of 20 items in which you choose 9, C(20, 9). Solving,

You can reduce the fraction in lots of ways — you have many combinations of the factors. But in any case, you should end up with all 1s in the denominator and numbers to multiply in the numerator.
The answer is 2,558,620,845.
It would be a wonder if anyone ever won this lottery! This problem involves a combination of 60 numbers, choosing 8. Solving,

The answer is 1,017,450.
Multiply C(10, 4) times C(20, 4). You’re simply multiplying the number of ways to choose four men times the number of ways to choose four women:
The answer is 83,218,600,080.
Solve C(400, 5):

Some scientific calculators have trouble with a number this large and may go into scientific notation for an answer. You may see something like 8.32186 x 1010.





