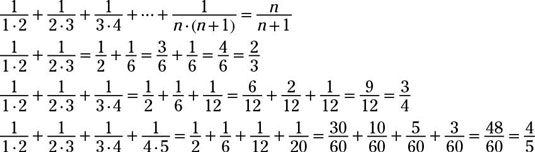Arithmetic sequences are very predictable. The terms are always a constant difference from one another. The terms in an arithmetic sequence are a1, a2, a3, . . . , an = a1, a1 + d, a1 + 2d, a1 + 3d, . . . , a1 + (n – 1)d. The number of times you add the common difference to the first term is 1 less than the total number of terms.
To find the sum of the terms of an arithmetic sequence, you can use one of these formulas:
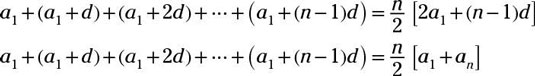
Finding the sum using either formula requires that you know how many terms are in the sequence. Solve for n, the number of terms, using the rule for the general term of the arithmetic sequence: an = a1 + (n – 1)d.
To find the sum of 4 + 10 + 16 + 22 + 28 + · · · + 304, you recognize that the first term, a1, is 4, the last term, an, is 304, and the difference between each pair of terms is 6. Solving 4 + (n – 1)6 = 304, you get 6n – 6 = 300; 6n = 306; n = 51. So, the sum of those 51 terms is
Geometrically speaking
Geometric sequences are almost as predictable as arithmetic sequences. The terms have a common ratio — you divide any term in a geometric sequence by the term that comes before it, and you get the same ratio or multiplier, no matter which two terms you choose.
The geometric sequence 1, 3, 9, 27, 81, . . . has a first term of 1 and a common ratio of 3. The general term for a geometric sequence is gn = g1(rn–1), where g1 is the first term and r is the common ratio.
To add up the first n terms of a geometric sequence, use this formula:
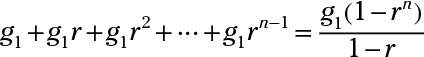
Adding up 1 + 3 + 9 + 27 + · · · + 6,561, you first determine that 6,561 is 38. This answer makes 6,561 the ninth term in the series, because 1(38) = 1(3n–1), and if 8 = n – 1, then n = 9. Using the formula for the sum,
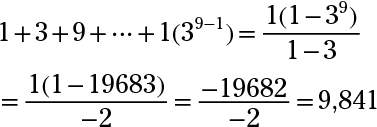
Easing into a sum for e
The number e is approximately equal to 2.718281828459. The value for e is irrational, which means that the decimal never ends or repeats. The number, however, is oh-so-necessary in the scientific, mathematical, and financial worlds.
You can determine the value for e using various formulas, one of which is the sum of a sequence of numbers. The more terms you add up in this series, the more correct decimal places for e you determine. The general term for this series is
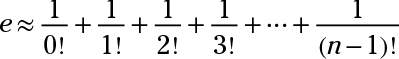
There is no handy formula for adding up the terms in this series, but a scientific calculator can do the job for a while. Here are a few of the sums:
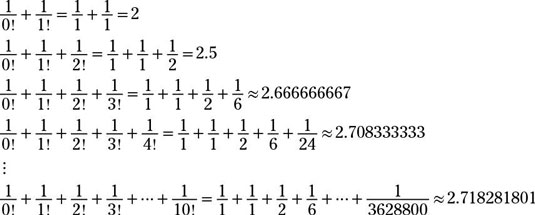
Signing in on the sine
The sine is one of the trigonometric functions. The input (x-value) for trig functions consists of angle measures. For instance, if y = sin x (sin is the abbreviation for sine) and x is 30 degrees, then y = sin 30 degrees = 0.5.
Several different methods are available for computing the value of the sine of an angle, but the one here is an infinite series of values. If you write the input, x, in radians instead of degrees (360 degrees = 2π radians), then
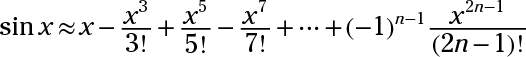
The more terms you use, the closer you get to the exact value of the function.
So, to find the sine of 30 degrees, change that measure to radians to get 30 degrees is approximately 0.5236 radians (30 degrees is one-twelfth of a circle, and
radians). Using the series,

In the fourth term, the number is so small that it rounds to 0 when you just want four decimal places.
Powering up on powers of 2
You can quickly and simply find the sum of a sequence consisting of powers of 2 just by finding the next power of 2 and subtracting 1. For instance, 1 + 2 + 4 + 8 + 16 consists of the powers of 2 from 20 to 24. The sum is 25 – 1 = 32 – 1 = 31. So, the rule is 1 + 2 + 4 + 8 + · · · + 2n = 2n+1 – 1.
Adding up fractions with multiples for denominators
Create a rather interesting sequence with
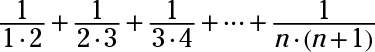
where you take the number of the term times the next integer and put their product in the denominator of a fraction. The sum of the terms is equal to
That result almost seems too easy to believe, doesn’t it? Look at a few examples: