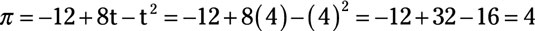An important factor influencing research and development costs is how much time you take for the project’s completion. A shorter time frame tends to increase research and development cost because you require more resources and false starts resulting in wasted effort are more likely. Thus, an inverse relationship exists between time and research and development costs. The time-cost trade-off function describes this relationship between time and development cost.
In addition to the time-cost trade-off in development cost, a project’s potential net revenue is also influenced by time. Because other firms also innovate, there is the possibility that their innovation makes your research and development project obsolete. Therefore, a development project of short duration is likely to have higher net revenue.
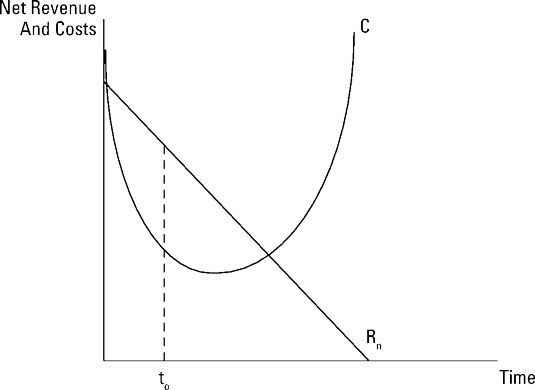
Based upon these two elements, you need to determine the optimal time frame for the project’s completion. The optimal time maximizes profit — the difference between net revenue and the time-cost trade-off function.
You want to choose a time span (t) for the project that maximizes profit — the difference between net revenue (Rn) and development cost (C). The optimal time span in the illustration is represented by t0 as it maximizes the difference between net revenue (Rn) and development cost (C). These is shown by the large gap or vertical difference between these two lines.
The expected net revenue, Rn, from your research and development project equals
where Rn represents net revenue in millions of dollars and t is time measured in years.
Your time-cost trade-off function is
where C is development cost in millions of dollars and t is again time.
In order to determine the optimal time frame for the project’s completion, take the following steps:
Note that the expected profit, ð, from the project equals net revenue minus the development cost represented by the time-cost trade-off function.
Thus,
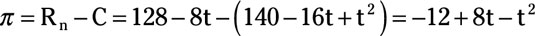
In order to maximize profit, take the derivative of profit, ð, with respect to time, t.
This derivative equals
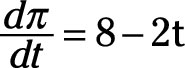
Set the derivative equal to zero and solve for t.
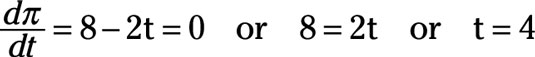
Thus, the project’s optimal time frame is four years. Substituting t equals 4 into the expected profit equation indicates that the expected profit is $4 million.