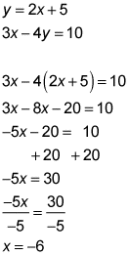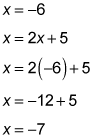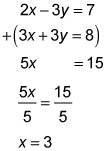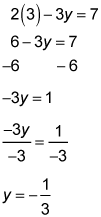TASC Math—Solving Systems of Equations through Substitution and Elimination

Using the substitution method

1. Solve one or both equations for one of the variables.
2. Substitute what one variable equals into the other equation.
3. Solve the resulting equation for that one variable.
4. Substitute the found value back into either original equation to solve for the second value.

Try this example:

y = 2x + 5

3x – 4y = 10

Because the first equation is already solved for y, you substitute what y equals into the second equation.

Now that you have a value for x, you can substitute it into either of the original equations.

So the solution to the system is (–6, –7). You can check this solution by substituting both values into both original equations.

Using the elimination method

1. Rewrite both equations so their variables are in the same order.
2. One pair of variables must have the same coefficients but with opposite signs. For example, if one equation has 2x, then the other equation needs to have –2x. If there isn't an existing pair of coefficients that meet this requirement, you must multiply or divide one or both equations.
3. Add the equations together; the pair identified in Step 2 should cancel.
4. Solve the produced equation for the remaining variable.
5. Substitute the value obtained in Step 4 back into one of the original equations.
6. Solve for the other variable.

Notice how the y's fit the requirement in Step 2. Add the two equations together.

Now that you have a value for x, you can substitute it back into either of the original equations.

The solution to the system is (3, –1/3).