You will likely get some rate, time, and distance problems on the PSAT/NMSQT. Don’t you hate questions in which one guy is driving east at 40 miles an hour and a friend is moving west doing 65? You’re supposed to figure out where they meet and ignore the fact that in real life they can just call each other and explain where they are.
But if you get one of these problems on the PSAT/NMSQT, at least you can solve it fairly easily. Just remember this formula: Rate x Time = Distance (RTD).
A little sketch or a chart often helps you with rate/time/distance questions.
Here’s an example. Your robot toddles along at a rate of 3 feet per minute for 30 minutes. MegaBrain’s robot zooms at 30 feet per second for 10 minutes. How much farther will MegaBrain’s robot travel than your robot?
To solve this one, try a chart. The headings match the terms of the formula, Rate x Time = Distance. Before you fill in the boxes, though, be sure that everything matches. MegaBrain’s robot travels 30 feet per second. (Watch out for these tricky changes in units!) Because a minute has 60 seconds, MegaBrain’s speed is 1800 feet per minute.
Now you can fill in the chart. Start with what you know:
| Rate | Time | Distance | |
|---|---|---|---|
| Your robot | 3 feet per minute | 30 minutes | |
| MegaBrain’s robot | 1800 feet per minute | 10 minutes |
Now fill in the empty squares. Your robot goes 3 x 30 or 90 feet. MegaBrain’s robot travels 1800 x 10 or 18,000 feet.
| Rate | Time | Distance | |
|---|---|---|---|
| Your robot | 3 feet per minute | 30 minutes | 90 |
| MegaBrain’s robot | 1800 feet per minute | 10 minutes | 18,000 |
MegaBrain’s robot travels 18,000 – 90 feet, or 17,910 feet farther than yours.
You may be asked how far apart they are. If so, note whether they’re traveling in the same direction or in the opposite direction. In the same direction, you subtract. In the opposite direction, you add. (Sketch it out and you’ll see.)
Hit the road and try these problems:
James and Kat are standing at opposite ends of a football field, 300 feet away from each other. If Kat walks at a rate of 12 feet per second, James walks at a rate of 8 feet per second, and they walk toward each other, how long will it take for them to meet up?
(A) 15 seconds
(B) 75 seconds
(C) 2 minutes
(D) 3 minutes
(E) 15 minutes
Two boats meet up in a lake, and after the captains share sandwiches, head off in different directions. The motorboat heads directly east at a rate of 36 miles per hour, and the sailboat goes north at a rate of 15 miles per hour. If both boats continue traveling in straight lines, how far apart will they be in 2 hours?
(A) 21 miles
(B) 39 miles
(C) 51 miles
(D) 78 miles
(E) 100 miles
Alexis walked at a rate of 3 miles per hour for 20 minutes and then stopped to talk on the phone for 16 minutes. After her phone conversation, Alexis walked at a rate of 5 miles per hour for the remainder of the hour. What was Alexis’s average speed over the hour?
(A) 2 mph
(B) 2.5 mph
(C) 3 mph
(D) 3.5 mph
(E) 4 mph
Now check your answers:
A. 15 seconds
You know that both James and Kat are walking for the same length of time, and you want to know what that time is, so for the moment, just call it t. James will walk (8 feet/second) x t feet (rate x time), and Kat will walk (12 feet/second) x t feet. Together, they walk 300 feet, so you know that 8t + 12t = 300.
Add together like terms and you get 20t = 300, and when you divide you see that t = 15. You can think about units by remembering that you’re dividing 300 feet by 20 feet/second, which works out to 15 seconds. Choice (A) is your answer.
D. 78 miles
RTD and right triangles? You can do it! Draw yourself a picture first.
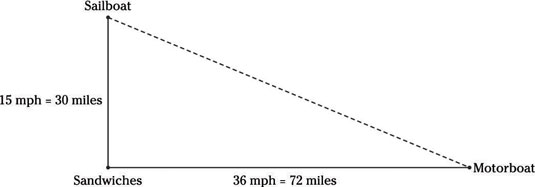
You know that each boat is traveling for 2 hours, so you can use RTD to determine how far each has traveled: 30 miles for the sailboat and 72 miles for the motorboat. Now all you need to do is apply the Pythagorean theorem to figure out how far apart the boats are: 302+ 722 = d2; 900 + 5184 = d2; d = 78 miles apart, Choice (D).
C. 3 mph
To find Alexis’s average speed, you first need to find the total distance she traveled and the total time that she was traveling (these both include the time that she was stopped!). For the first part of her trip, Alexis traveled for 20 minutes, or 1/3 of an hour, at a rate of 3 miles per hour.
Using RTD, you can see that she traveled 1 mile during those first 20 minutes. Alexis didn’t make forward progress during her phone conversation, so you know that she spent the first 36 minutes going 1 mile. In the remaining 24 minutes (60 – 36 = 24 minutes) of the hour, Alexis walked at a rate of 5 miles per hour.
24 minutes out of 60 is the same as 2/5 of an hour. Using RTD, (2/5) x 5 = 2 miles of travel during the last 24 minutes, for a total of 3 miles in 60 minutes. This makes Alexis’s average speed 3 miles per hour, Choice (C).




