Hooke’s law says that
F = –kx
where F is the force exerted by the spring, k is the spring constant, and x is displacement from equilibrium. Because of Isaac Newton, you know that force also equals mass times acceleration:
F = ma
These force equations are in terms of displacement and acceleration, which you see in simple harmonic motion in the following forms:

Inserting these two equations into the force equations gives you the following:

You can now find the angular frequency (angular velocity) of a mass on a spring, as it relates to the spring constant and the mass. You can also tie the angular frequency to the frequency and period of oscillation by using the following equation:
![]()
With this equation and the angular-frequency formula, you can write the formulas for frequency and period in terms of k and m:

Say that the spring in the figure has a spring constant, k, of 15 newtons per meter and that you attach a 45-gram ball to the spring.
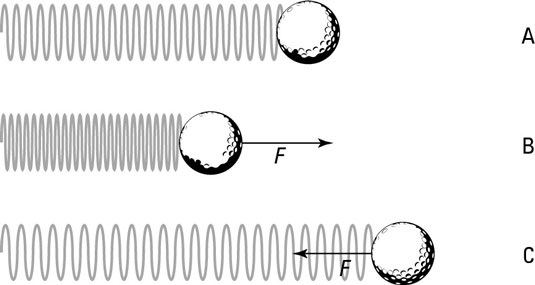

The period of the oscillation is 0.34 seconds. How many bounces will you get per second? The number of bounces represents the frequency, which you find this way:
![]()
You get nearly 3 oscillations per second.
Because you can relate the angular frequency,
to the spring constant and the mass on the end of the spring, you can predict the displacement, velocity, and acceleration of the mass, using the following equations for simple harmonic motion:

Using the example of the spring in the figure — with a spring constant of 15 newtons per meter and a 45-gram ball attached — you know that the angular frequency is the following:
![]()
You may like to check how the units work out. Remember that
![]()
so the units you get from the equation for the angular velocity work out to be

Say, for example, that you pull the ball 10.0 centimeters before releasing it (making the amplitude 10.0 centimeters). In this case, you find that






